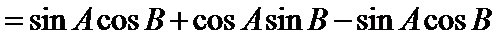函数y＝Asin(ωx＋φ)的应用
共45题

· 函数y＝Asin(ωx＋φ)的应用

函数y＝Asin(ωx＋φ)的应用
共45题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

12.已知函数为的零点，为图像的对称轴，且在单调，则的最大值为( )

A11

正确答案

知识点

函数y=Asin（ωx+φ）的图象变换函数y＝Asin(ωx＋φ)的应用

题型：单选题

单选题 · 5 分

3．为了得到函数的图象，只需把函数的图象上所有的点

A向左平行移动个单位长度

B向右平行移动个单位长度

C向左平行移动个单位长度

D向右平行移动个单位长度

正确答案

知识点

正弦函数的图象函数y＝Asin(ωx＋φ)的应用

题型：简答题

简答题 · 12 分

设△ABC的内角A,B,C的对边分别为，.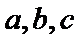

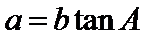
18.证明：;

19.若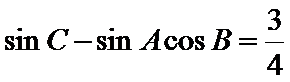 ,且B为钝角，求A,B,C.

第(1)小题正确答案及相关解析

正确答案

由及正弦定理得，所以。

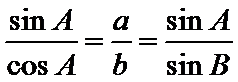
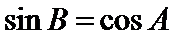
解析

见答案

考查方向

本题主要考察正弦定理及其应用，意在考察考生的运算求解能力和转化能力。

解题思路

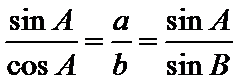
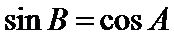
由题及正弦定理得可得。

易错点

不会想到切割化弦；

第(2)小题正确答案及相关解析

正确答案

,,.

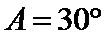
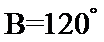
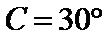
解析

因为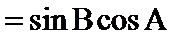，所以，

由（1）知，因此，又B为钝角，所以，

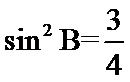
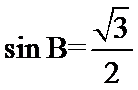
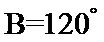
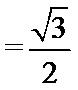
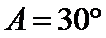
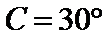
故，由知，从而，

综上所述，,,.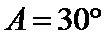

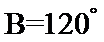
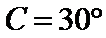
考查方向

本题主要考察正弦定理及其应用，意在考察考生的运算求解能力和转化能力。

解题思路

由两角和与差的公式化简得，结合（1）得，又B为钝角，所以求出角，进而可以求出角A,C。

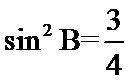
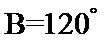
易错点

做第（2）问时联系不上第（1）问的结论。

题型：单选题

单选题 · 5 分

4.使函数是奇函数，且在上是减函数的的一个值是（）

正确答案

解析

考查方向

本题主要考察了求函数y＝Asin(x＋)的解析式，考察了正弦函数的奇偶性，考察了特殊角的三角函数值求解，主要考察学生对三角函数的图像及性质的理解，本题较简单

解题思路

1、通过和角公式求函数y＝Asin(x＋)的解析式，

2、利用函数奇偶性以及在上为减，确定在原点处对称中心为减区间上的零点得出关于的关系，

3，根据选项得出结果

易错点

本题易于在求解时，单调性的作用

知识点

正弦函数的单调性函数y＝Asin(ωx＋φ)的应用

题型：单选题

单选题 · 5 分

椭圆的离心率为，若直线与其一个交点的横坐标为，则的值为

正确答案

解析

因为椭圆的离心率为，所以有，即，，所以。当时，交点的纵坐标为，即交点为，代入椭圆方程，即，所以，选C.

知识点

函数y＝Asin(ωx＋φ)的应用

题型：简答题

简答题 · 12 分

在中，的对边的边长分别为且成等比数列。

（1）求角B的取值范围;

（2）若关于B的不等式恒成立，求m的取值范围。

正确答案

（1）（2）

解析

解析：（1）

当且仅当时，故………5分

（2）

＝……8分

故原不等式恒成立，即得

的取值范围为.…12分

知识点

函数y＝Asin(ωx＋φ)的应用

题型：单选题

单选题 · 5 分

如下图，某几何体的正视图与侧视图都是边长为1的正方形，且体积是，则该几何体的俯视图可以是

正确答案

解析

若俯视图为A,则几何体为边长为1的正方体，所以体积为1，不满足条件；若为B,则该几何体为底面直径为1，高为1的圆柱，此时体积为，不满足条件；若为D, 几何体为底面半径为1，高为1的圆柱的部分，此时体积为，不满足条件，若为C，该几何体为底面是直角三角形且两直角边为1，高为1的三棱柱，所以体积为，满足条件，所以选C.

知识点

函数y＝Asin(ωx＋φ)的应用

题型：简答题

简答题 · 10 分

自圆外一点引圆的一条切线，切点为，为的中点，过点引圆的割线交该圆于两点，且，.

（1）求证：与相似；

（2）求的大小。

正确答案

见解析。

解析

（1）因为为圆的切线，所以.

又为中点，所以.

因为，所以与相似.（5分）

（2）由（1）中与相似，可得.

在中，由，

得. (10分)

知识点

函数y＝Asin(ωx＋φ)的应用

题型：单选题

单选题 · 5 分

一个底面为正三角形且侧棱垂直于底面的三棱柱内接于半径为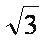的球，则该棱柱体积的最大值为（）

正确答案

解析

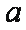
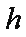
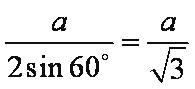
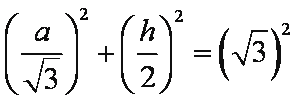
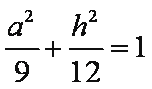
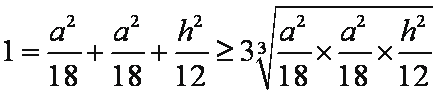
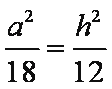
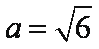
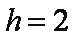
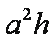
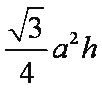
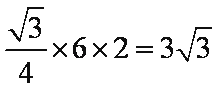
设该三棱柱的底面边长为，高为，则底面正三角形的外接圆半径是，依题意有，即，，当且仅当，即，时取等号，此时取得最大值，因此该棱柱的体积的最大值是.

知识点

函数y＝Asin(ωx＋φ)的应用

题型：单选题

单选题 · 5 分

在△ABC中，已知•=9，sinB=cosA•sinC，S△ABC=6，P为线段AB上的点，且=x+y，则xy的最大值为（　　）

正确答案

解析

解：△ABC中设AB=c，BC=a，AC=b

∵sinB=cosA•sinC，sin（A+C）=sinCcosnA，即sinAcosC+sinCcosA=sinCcosA

∴sinAcosC=0

∵sinA≠0∴cosC=0 C=90°

∵•=9，S△ABC=6

∴bccosA=9，bcsinA=6

∴tanA=，根据直角三角形可得sinA=，cosA=，bc=15

∴c=5，b=3，a=4

以AC所在的直线为x轴，以BC所在的直线为y轴建立直角坐标系可得C（0，0）A（3，0）B（0，4）

P为线段AB上的一点，则存在实数λ使得=（3λ，4﹣4λ）（0≤λ≤1）

设，则||=||=1，

=（1，0），=（0，1），

∴=x+y=（x，0）+（0，y）=（x，y）可得x=3λ，y=4﹣4λ则4x+3y=12，

12=4x+3y≥，xy≤3

故所求的xy最大值为：3。

故选C。

知识点

函数y＝Asin(ωx＋φ)的应用

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 理科数学 > 函数y＝Asin(ωx＋φ)的应用

扫码查看完整答案与解析