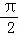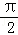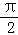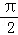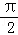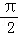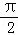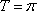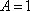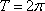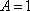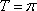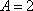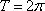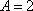- 函数的单调性及单调区间
- 共78题
函数f(x)=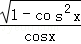
正确答案
解析
∵ 函数f(x)=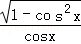
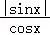
由于当 0<x<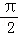
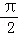
知识点
已知函数


(1)求函数
(2)求证:当


正确答案
见解析
解析
(1)函数


当
当


当
当


综上所述,
当




当




……………………………………5分
(2)由(1)可知,当






所以

因为

令

①当




所以函数


所以
因为
所以对于任意

②当


所以函数


所以对于任意

综上所述,对于任意

知识点
已知函数f(x)是定义(0,+∞)的单调递增函数,且x∈N*时,f(x)∈N*,若f[f(n)]=3n,则f(2)=_________;f(4)+f(5)=_________。
正确答案
3;15
解析
若f(1)=1,则f(f(1))=f(1)=1,与条件f(f(n))=3n矛盾,故不成立;
若f(1)=3,则f(f(1))=f(3)=3,即f(1)=f(3)这与函数单调递增矛盾,故不成立;
若f(1)=n (n>3),则f(f(1))=f(n)=3,与f(x)单调递增矛盾,故不成立;
所以只剩f(1)=2,代入可得f(f(1))=f(2)=3,
进而可得f(f(2))=f(3)=6,f(f(3))=f(6)=9,
由单调性可知f(4)=7,f(5)=8,故f(4)+f(5)=15
知识点
设函数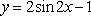
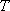
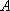
正确答案
解析
略
知识点
已知函数



正确答案
解析
略
知识点
扫码查看完整答案与解析