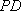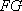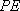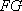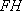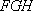- 两条直线平行的判定
- 共27题
如图,PA垂直于矩形ABCD所在的平面,
(1)求证:AF//平面PCE;
(2)求证:平面
(3)求四面体PEFC的体积.
正确答案
见解析。
解析
知识点
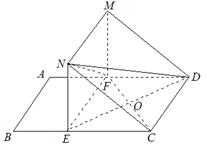
如图,已知四边形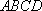
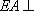

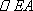

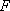
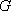
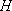
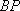
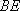
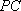
(1)求证:
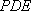
(2)求证:平面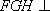
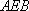
(3)在线段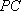
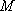
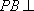
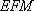
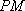
正确答案
见解析
解析
(1)证明:因为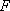
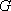
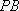
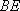
所以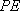
又因为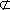
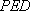


所以
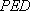
(2)因为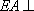

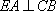
又因为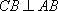
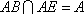
所以

由已知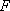
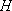
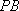
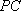
所以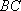
则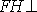
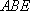
而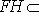
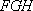
所以平面
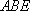
(3)在线段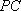
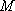
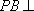
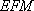
在直角三角形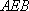
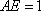
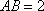
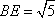
在直角梯形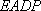
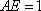
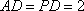
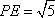
所以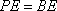
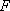
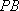

要使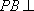
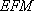
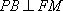
因为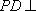
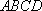
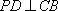
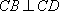
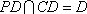
所以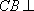
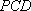
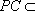
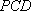
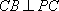
若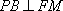
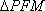
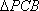
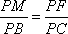
由已知可求得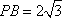
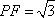
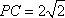

知识点
如图,四边形ABCD是菱形,四边形MADN是矩形,平面MADN
(1)EF//平面MNCB;
(2)平面MAC
正确答案
见解析。
解析
知识点
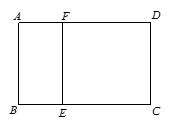
在如图所示的几何体中,四边形是ABEF长方形,DA⊥平面,ABEF,BC//AD,G,H分别为DF,CE的中点,且AD=AF=2BC。
(1)求证:GH//平面ABCD;
(2)求三棱锥与的体积之比。
正确答案
见解析。
解析
知识点
如图,直三棱柱ABC﹣A1B1C1中,△ABC是等边三角形,D是BC的中点。
(1)求证:直线A1D⊥B1C1;
(2)判断A1B与平面ADC1的位置关系,并证明你的结论。
正确答案
见解析
解析
(1)在直三棱柱ABC﹣A1B1C1中,AA1⊥面ABC,∴ AA1⊥BC,
在等边△ABC中,D是BC中点,∴ AD⊥BC
∵ 在平面A1AD中,A1A∩AD=A,∴BC⊥面A1AD
又∵ A1D⊂面A1AD,∴ A1D⊥BC
在直三棱柱ABC﹣A1B1C1中,四边形BCC1B1是平行四边形,∴ B1C1∥BC
∴ A1D⊥B1C1
(2) 在直三棱柱ABC﹣A1B1C1中,四边形ACC1A1是平行四边形,
在平行四边形ACC1A1中联结A1C,交于AC1点O,连接DO。
故O为A1C中点。
在三角形A1CB中,D 为BC中点,O为A1C中点,∴DO∥A1B。
因为DO⊂平面DAC1,A1B⊄平面DAC1,∴A1B∥面ADC1
∴ A1B与面ADC1平行。
知识点
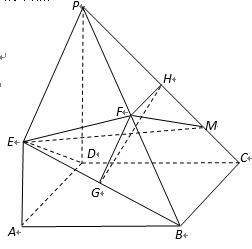
如图4,在四棱锥





(1)求证:

(2)求证:
(3)若


正确答案
见解析。
解析
知识点
如图,菱形









(1)求证:

(2)求证:平面

(3)求三棱锥
正确答案
见解析
解析
(1)证明:因为点

所以



所以


因为



所以

(2)证明:由题意,
因为


又因为菱形

因为
所以

因为

所以平面

(3)解:三棱锥

由(2)知,

所以



所求体积等于
知识点
如图,矩形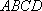
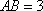
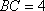
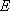
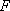
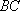
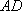
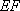
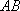
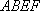
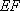

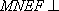
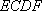
(1)求证: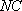

(2)若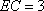
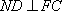
(3)求四面体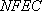
正确答案
见解析
解析
(1)证明:因为四边形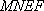
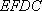
所以 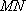
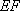

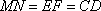
所以 四边形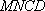
所以 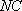
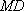
因为 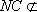
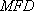
所以 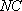
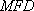
(2)证明:连接
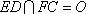
因为平面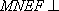
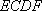
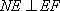
所以 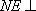
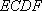
所以 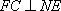
又 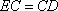
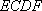
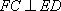
所以 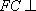
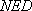
所以 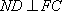
(3)解:设
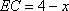
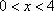
由(1)得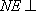
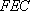
所以四面体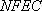
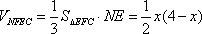
所以 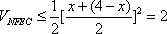
当且仅当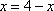
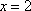
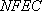
知识点
如图,在平面直角坐标系xOy中,F1,F2分别为椭圆




正确答案
解析
因为BF1=BF2=a,F1F2=2c,由余弦定理得


直线BF2的斜率为
设D(


又D在椭圆上,故
得

知识点
18.把一颗骰子投掷两次,第一次出现的点数记为





(Ⅰ)直线

(Ⅱ)直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析