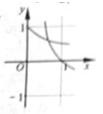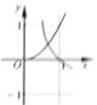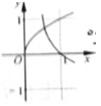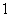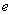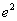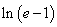- 对数与对数函数
- 共252题
8.若a>b>0,0<c<1,则( )
正确答案
知识点
15.若不等式logax>sin2x(a>0,a≠1)对任意x∈(0,
正确答案
解析
记y1=logax,y2=sin2x,原不等式相当于y1>y2
作出两个函数的图象,如图所示
可知当y1=logax过点A(
所以当

知识点
11.设



则下列关系式中正确的是( )
正确答案
解析
然后再比较
利用均值不等式得到

自然对数底数大于1,所以单调递增,所以
考查方向
解题思路


易错点
对数的基本运算不会,判断不出

知识点
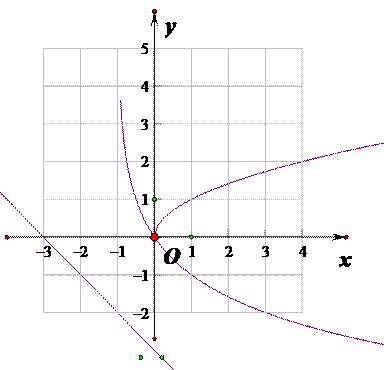
在同一直角坐标系中,函数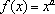
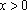
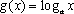
正确答案
解析
对A,没有幂函数的图象,;对B,
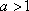
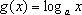
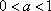

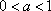
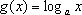
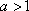
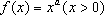
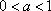
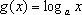
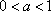
知识点
已知函数

正确答案
解析
略
知识点
已知函数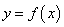
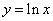
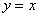
正确答案
解析
略
知识点
已知函数


(1)求函数

(2) 设函数


正确答案
(1)


解析
(1) 




由


(2) 答:函数

理由:由(1)可知,
可求得函数

对任意

所以,函数
当




于是,

因此,函数

依据奇函数的性质,可知, 函数

知识点
已知函数
(1) 求f(x)的反函数的图象上图象上点(1,0)处的切线方程;
(2)证明: 曲线y = f (x) 与曲线
(3)设a<b, 比较

正确答案
见解析
解析
(1) f (x)的反函数


(2) 证明曲线y=f(x)与曲线
因此,
所以,曲线y=f(x)与曲线
(3)设
令


所以
知识点
6.函数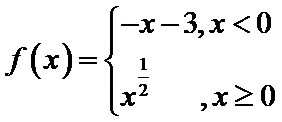
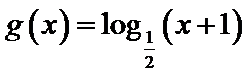
正确答案
解析
根据题意可知
考查方向
解题思路
【解题思路】本题函数的单调性及其性质解题,
画出函数图像不难分析得出答案,如图:
易错点
该题出错在分段不清,对数函数不熟悉
知识点
9.已知



正确答案
解析
因为








考查方向
本题主要考查了函数的单调性和比较大小。
易错点
本题易在判定
知识点
扫码查看完整答案与解析