函数奇偶性的性质
共128题

· 函数奇偶性的性质

函数奇偶性的性质
共128题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

6.定义在上的偶函数满足：，若在区间内单调递增，则、、的大小关系为（）

正确答案

解析

由知，所以函数f(x)的周期为2，从而有，。又由在区间内单调递增知，所以。因此A选项不正确，B选项不正确，D选项不正确，所以选C选项。

考查方向

本题主要考查了函数的奇偶性、周期性，单调性,在近几年的各省高考题出现的频率较高，常与把函数单调性、周期性、对称型、奇偶性等知识点综合在一起命题。

解题思路

由题意知f(x)是以2为周期的函数，又由在区间内单调递增且有，知，因此A选项不正确，B选项不正确，D选项不正确，所以选C选项。

易错点

1、不能正确处理导致对三者不能进行转化。

知识点

函数单调性的性质函数奇偶性的性质

题型：填空题

填空题 · 5 分

12．已知函数.若，则．

正确答案

解析

根据题意可构造奇函数，由，所以，又为奇函数，则，所以。

考查方向

本题主要考查了考生构造奇函数和整体换元法的能力。

解题思路

先构造，可知为奇函数，由题可得的值，从而得到的值，易得的值。

易错点

本题易在构造奇函数时发生错误。

知识点

函数奇偶性的性质

题型：单选题

单选题 · 5 分

9.若为偶函数，则的解集为（）

正确答案

解析

若f(x)=为偶函数，则f(x)=f(-x),即,(1-a)(-)=0,a=1, f(x)=, f(x-1)< ,，(-1)(，0

考查方向

函数的奇偶性，解不等式

解题思路

先由偶函数性质，求出a=1，将不等式进行化简整理，(-1)(，解出取值范围，进而求出x的取值范围

易错点

不等式的化简整理

知识点

函数奇偶性的性质不等式的性质

题型：单选题

单选题 · 5 分

10．已知函数，如果存在实数，使得对任意的实数，都有成立，则的最小值为

正确答案

知识点

函数奇偶性的性质

题型：单选题

单选题 · 5 分

10．已知定义域为R的偶函数满足对任意的，

有，且当时，。若函数在上恰有三个零点，则实数的取值范围是

正确答案

解析

，

且是定义域为的偶函数，

令可得，

又，

则有，

是最小正周期为2的偶函数．

当时，，

若，则，

则，

即，，

若，则，

即，

即，，

综上，，

由函数，

得函数，

设，

作出函数和的图象如图，

要使函数在上恰有三个零点，

则，

当，则，

则，，

当，则，

则，，

由整理得，

由判别式，

整理得得（由图象知不合适）或，

由整理得，

由判别式，

整理得得（由图象知不合适）或，综上，要使函数在上恰有三个零点，则实数的取值范围是。所以选B项。

考查方向

本题主要考查根的存在性及根个数的判断。

解题思路

1）由已知的单调性奇偶性，球的函数的解析式；

2）解方程得到关于的一元二次方程

3）用判别式可得的范围。

易错点

本题易在求函数解析式时出现错误。

知识点

函数奇偶性的性质函数零点的判断和求解

题型：填空题

填空题 · 5 分

12. 定义在上的奇函数在区间上单调递减，且，则不等式的解集为 .

正确答案

解析

由奇函数在区间上单调递减，所以函数在区间上也单调递减，且。

（1）当即时，不等式可化为，而，所以成立，符合题意。

（2）当即时，不等式可化为，所以。

（3）当即时，

①当时，不等式可化为，所以。

②当时，不等式可化为，所以符合题意。

③当时，不等式可化为，所以与取交集为。

综上可知，的解集合为。

考查方向

本题主要考查函数的奇偶性，抽象函数的图像等知识，意在考查考生分类讨论的思想。

解题思路

1.先利用奇函数求出函数在对称的区间上的单调性；

2.根据x的范围不同分类求出x的解后取并集。

易错点

1.不会奇函数在对称的区间上单调性相同这个结论；

2.分类讨论时不全或重复。

知识点

函数奇偶性的性质函数性质的综合应用不等式与函数的综合问题

题型：填空题

填空题 · 5 分

13.已知是定义在上的奇函数，当时，，则= .

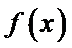
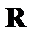
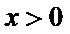
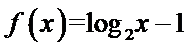
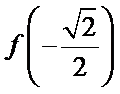
正确答案

；

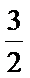
解析

=。

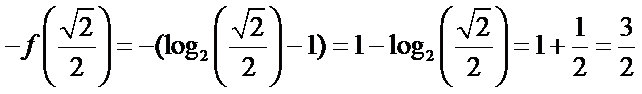
考查方向

本题主要考查函数的奇偶性和对数的运算性质等知识，意在考查考生的运算求解能力和转化与化归的能力。

解题思路

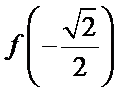
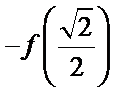
先利用奇偶性将转化为；2.带入解析式求解即可。

易错点

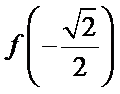
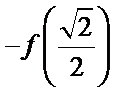
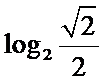
1.不会利用奇偶性将转化为；2.不会求的值；

知识点

函数奇偶性的性质函数的值

题型：单选题

单选题 · 5 分

12.设函数是奇函数的导函数，，当时，，则使得成立的的取值范围是

正确答案

解析

设，则的导数为：

∵当时总有成立，

即当时，，

∴当时，函数为增函数，

又∵

∴函数为定义域上的偶函数，

∴时，函数是减函数，

又∵

∴时，由，得：，解得：，

时，由，得：，解得：，

∴成立的x的取值范围是：

故选B.

考查方向

本题考查了利用导数判断函数的单调性，并由函数的奇偶性和单调性解不等式的应用问题，是综合题目．

解题思路

构造函数g(x)，利用g(x)的导数判断函数g(x)的单调性与奇偶性，求出不等式的解集即可．

易错点

本题的难点和易错点在于函数g(x)的构造.

知识点

函数奇偶性的性质导数的运算其它不等式的解法

题型：简答题

单选题

根据《中华人民共和国广告法》，不得发布广告的药品为

A．人血白蛋白
B．氨茶碱
C．可待图片
D．狂犬疫苗
E．龙胆泻肝九

正确答案

解析

禁止发布广告的药品包括：麻醉药品、精神药品、医疗用毒性药品、放射性药品。可待因片属于麻醉药品，故选C。

题型：填空题

填空题 · 5 分

9. 定义在上的偶函数，当时，，则在上

的零点个数为个

正确答案

解析

因为，所以当时，在上递减，在上递增，且最小值为，又因为，所以时有两个零点，又因为为R上的偶函数，所以在上的零点个数为4个。

考查方向

①函数的综合应用②复合函数的单调性③偶函数的应用。

解题思路

判断时函数的单调性以及最值情况，结合，得出时有两个零点，进而知道在上的零点个数为4个。

易错点

①注意不到的正负导致不严密②单调性判断有误

知识点

函数奇偶性的性质函数零点的判断和求解

棒棒哒，已学完当前知识点学习下一知识点

下一知识点 : 奇偶函数图象的对称性

百度题库 > 高考 > 理科数学 > 函数奇偶性的性质

扫码查看完整答案与解析