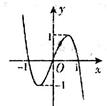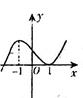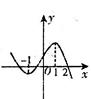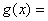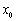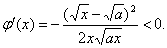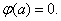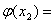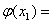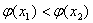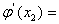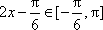- 奇偶函数图象的对称性
- 共31题
9.建设服务政府要加强政府公共服务职能。以下体现履行这一职能的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
已知函数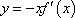


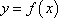
正确答案
解析
略
知识点
已知函数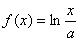
(1)若曲线
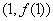
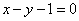

(2)设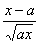

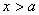
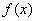
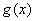
(3)当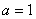
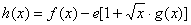


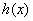
求证:对于曲线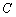
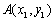
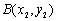
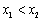

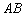
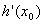
正确答案
见解析。
解析
(1)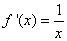
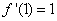
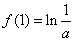
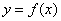
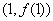
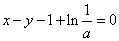
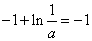
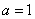
(2)

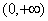

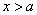
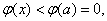


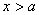

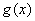
(3) 由题,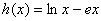
∵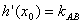

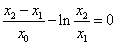
即
设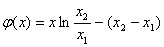


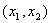
只需证明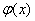
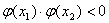

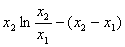
为了判断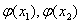
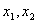

讨论他们的最值:
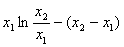
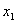
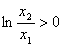
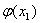
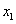
∵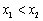
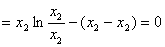
同理:

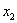
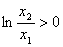

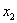
∵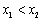
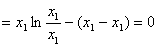
∴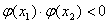
∴函数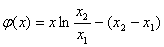
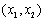

又
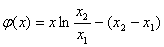

∴函数


知识点
函数
正确答案
解析
略
知识点
已知圆



正确答案
解析
略
知识点
已知函数






正确答案
-3
解析
略
知识点
已知:函数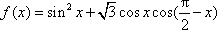
(1)求函数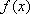
(2)当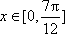

正确答案
(1)
(2)函数

解析
(1)

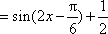
函数关于直线 
所以 对称轴方程为 
(2)当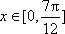
由函数图象可知,
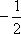
所以函数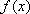


知识点
已知抛物线C的顶点是椭圆
(1)求抛物线C的方程;
(2)若
(ⅰ)设
(ⅱ)若a=-1,点A关于x轴的对称点为D,证明:直线BD过定点。
正确答案
见解析。
解析
(1)由题意,设抛物线C的标准方程为y2=2px(x>0),焦点F(
∵椭圆
∴
∴抛物线方程为:y2=4x …………4分
(2)(ⅰ)设直线AB:my=x一a。
联立

设A(x1,y1),B(x2,y2),则y1y2=一4a,
由S△AOB=
=
∴
∵
∴
∴当a=2时,t有最小值一2. …………10分
(ⅱ)由(ⅰ)可知D(x1,一y1),

直线BD的方程为y一y2=
即
y=
∴y=
∴直线BD过定点(1,0)…………………………14分
知识点
7.若函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.函数









正确答案
解析
知识点
扫码查看完整答案与解析