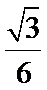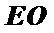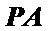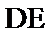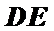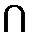- 空间向量及其应用、空间角
- 共58题
4.已知菱形



正确答案
解析
∵菱形ABCD的边长为a,∠ABC=60°,∴








菁优网版权所有【解题思路】由已知可求






考查方向
易错点
平面向量数量积的运算,线性转换.
知识点
9.已知










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
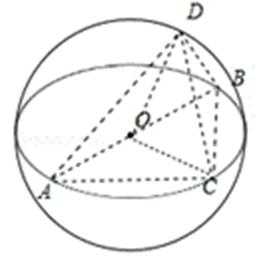
15.半径为1的球面上有四个点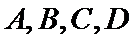
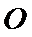
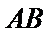
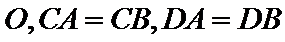
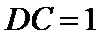
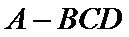
正确答案
解析
由题意可知图形如图所示,
AB过点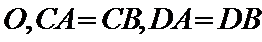
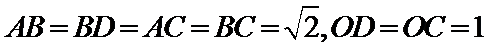
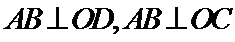
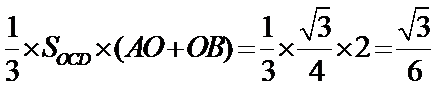
考查方向
解题思路
根据图中的有关关系,确定图形的特征,将三棱锥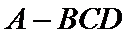
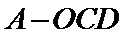
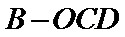
易错点
本题容易因对球面上的问题想象不到位,不能很好地寻求分割图形的策略而导致错误的出现。
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
已知平面内点A,B,O不共线,
正确答案
解析
略
知识点
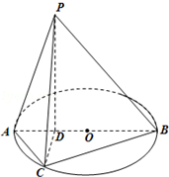
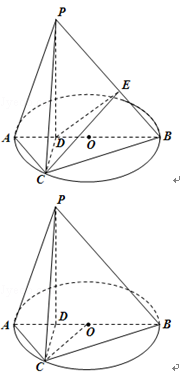
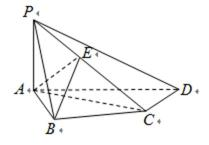
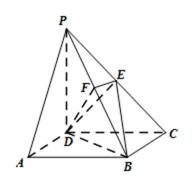
如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD=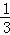
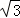
(1)求证:PA⊥CD;
(2)求二面角C﹣PB﹣A的余弦值。
正确答案
见解析。
解析
(1)连接OC,由3AD=BD知,点D为AO的中点,
又∵AB为圆的直径,∴AC⊥BC,
∵
∴△ACO为等边三角形,∴CD⊥AO.
∵点P在圆O所在平面上的正投影为点D,
∴PD⊥平面ABC,又CD⊂平面ABC,
∴PD⊥CD,PD∩AO=D,
∴CD⊥平面PAB,PA⊂平面PAB,
∴PA⊥CD.
(2)过点D作DE⊥PB,垂足为E,连接CE,
知识点
如图,在四棱锥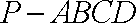
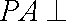




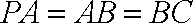


(1)证明:
(2)证明:

(3)求二面角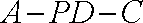
正确答案
见解析
解析
(1)证明:在四棱锥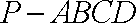
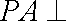



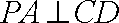
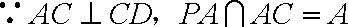

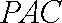
而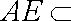
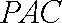

(2)证明:由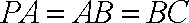

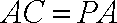
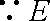


由(1)知,

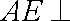

而





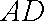


又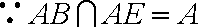

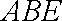
(3)解法一:过点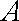

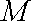

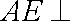

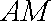



因此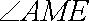
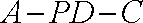
由已知,得
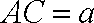
可得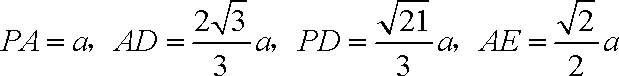
在
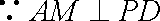

则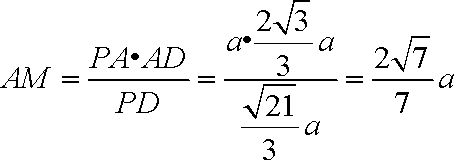
在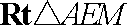
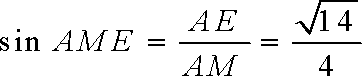
所以二面角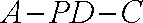
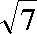
解法二:由题设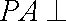

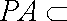
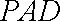



过点
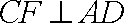
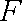
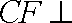
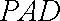
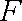

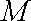
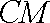


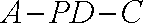
由已知,可得
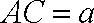
可得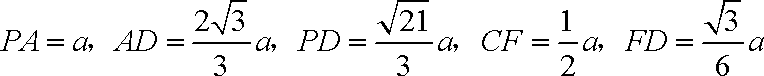
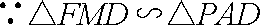
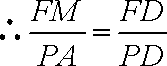
于是,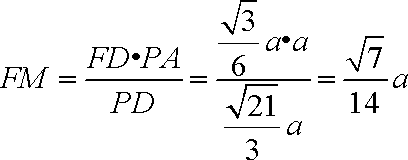
在

所以二面角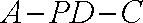
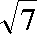
知识点
如图,在四棱锥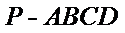
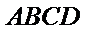
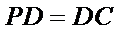
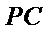
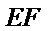
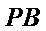
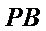
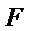
17.证明: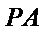
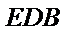
18.证明: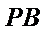
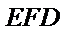
正确答案
详见解析
解析
证明:(1)连结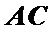
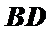
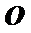
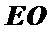
∵底面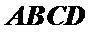
∴点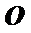
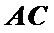
又∵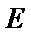
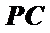
∴在△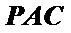
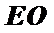
∴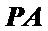
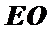
而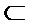
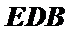
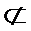
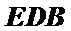
∴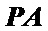
考查方向
直线与平面平行的判定;棱柱、棱锥、棱台的体积;直线与平面垂直的判定
解题思路
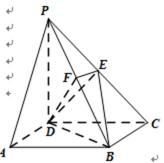
由题意连接AC,AC交BD于O,连接EO,则EO是中位线,证出PA∥EO,由线面平行的判定定理知PA∥平面EDB
易错点
空间立体感不强,逻辑分析能力弱
正确答案
详见解析
解析
(2)由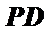
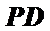
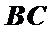
∵底面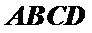
∴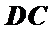
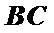
∴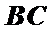
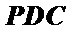
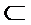
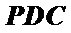
∴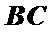
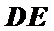
∵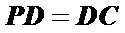
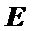
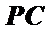
∴△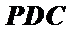
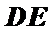
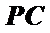
由①和②得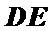
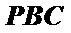
而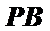
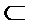
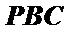
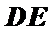
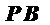
又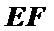
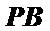
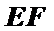
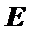
∴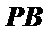
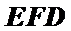
考查方向
直线与平面平行的判定;棱柱、棱锥、棱台的体积;直线与平面垂直的判定
解题思路
由PD⊥底面ABCD得PD⊥DC,再由DC⊥BC证出BC⊥平面PDC,即得BC⊥DE,再由ABCD是正方形证出DE⊥平面PBC,则有DE⊥PB,再由条件证出PB⊥平面EFD
易错点
空间立体感不强,逻辑分析能力弱
已知球O夹在一个锐二面角



正确答案
3(4)π
解析
解析:设球的半径为r.过球心O作直线l的垂线,设垂足为C,则三角形OAC是以角A为直角的直角三角形,且OA=r,OC=,点A到OC的距离为5(5),设AC的长为x,则xr=5(5)×=2,x2+r2=5,两式联立解得r=1(x=2,)或r=2(x=1,)(因为二面角为锐二面角,故舍去),所以球的体积为3(4)π。
知识点
18.如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD//BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
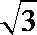
(1)若点M是棱PC的中点,求证:PA // 平面BMQ;
(2)求证:平面PQB⊥平面PAD;
(3)若二面角M-BQ-C为30°,设PM=tMC,试确定t的值 .
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析