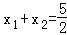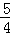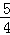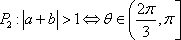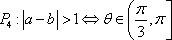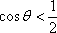- 平行关系的综合应用
- 共162题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
集合
正确答案
解析


知识点
如图,ABEDFC为多面体,平面ABED与平面ACFD垂直,点O在线段AD上,OA=1,OD=2,⊿OAB, ⊿OAC, ⊿ODE, ⊿ODF都是正三角形.
(1)证明直线BC∥EF;
(2)求棱锥F-OBED的体积.
正确答案
见解析。
解析
(1)(综合法)
证明:设G是线段DA与线段EB延长线的交点,由于△OAB与△ODE都是正三角形,所以OB∥

同理,设G′是线段DA与线段FC延长线的交点,有OG′=OD=2,又由于G和G′都在线段DA的延长线上,所以G与G′重合。
在△GED和△GFD中,由OB∥



(向量法)
过点F作FQ⊥AD,交AD于点Q,连QE,由平面ABED⊥平面ADFC,知FQ⊥平面ABED,以Q为坐标原点,


由条件知E(





则有,

所以
(2)解:由OB=1,OE=2,∠EOB=60°,知SEOB=


过点F作FQ⊥AD,交AD于点Q,由平面ABED⊥平面ACFD知,FQ就是四棱锥F-OBED的高,且FQ=


知识点
(1)设x≥1,y≥1,证明
(2)设1<a≤b≤c,证明
正确答案
见解析。
解析
(1)由于x≥1,y≥1,所以
将上式中的右式减左式,得
既然x≥1,y≥1,所以
(2)设
于是,所要证明的不等式即为
其中
故由(1)立知所要证明的不等式成立。
知识点
已知f(x),g(x)分别是定义在R上的偶函数和奇函数,且f(x)-g(x)=x3+x2+1,则f(1)+g(1)=( )。
正确答案
解析
由f(x)与g(x)分别是定义在R上的偶函数和奇函数,知f(-1)=f(1),g(-1)=-g(1)。
又由f(x)-g(x)=x3+x2+1,
令x=-1,得f(-1)-g(-1)=(-1)3+(-1)2+1=1,
即f(1)+g(1)=1.故选C.
知识点
已知F是抛物线y2=x的焦点,A,B是该抛物线上的两点,|AF|+|BF|=3,则线段AB的中点到y轴的距离为( )
正确答案
解析
∵F是抛物线y2=x的焦点
F(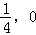
设A(x1,y1) B(x2,y2)
∴|AF|+|BF|=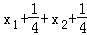
解得
∴线段AB的中点横坐标为
∴线段AB的中点到y轴的距离为
故选C
知识点
在平面直角坐标系xOy中,已知点A(0,-1),B点在直线y = -3上,M点满足

(1)求C的方程;
(2)P为C上的动点,l为C在P点处得切线,求O点到l距离的最小值。
正确答案
(1)曲线C的方程式为y=

(2)o点到
解析
(1)设M(x,y),由已知得B(x,-3),A(0,-1)。
所以


再由题意可知(


所以曲线C的方程式为y=

(2)设P(x







因此直线


则o点到


当

知识点
设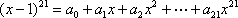
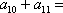
正确答案
0
解析
略
知识点
不等式组的解集记为D,有下面四个命题:
p1:∀(x,y)∈D,x+2y≥-2,
p2:∃(x,y)∈D,x+2y≥2,
p3:∀(x,y)∈D,x+2y≤3,
p4:∃(x,y)∈D,x+2y≤-1.
其中的真命题是( )
正确答案
解析
不等式组表示的区域D如图中的阴影部分所示,设目标函数z=x+2y,根据目标函数的几何意义可知,目标函数在点A(2,-1)处取得最小值,且zmin=2-2=0,即x+2y的取值范围是[0,+∞),故命题p1,p2为真,命题p3,p4为假。
知识点
已知a与b均为单位向量,其夹角为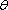
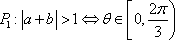
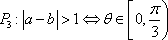
其中的真命题是
正确答案
解析
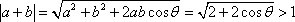
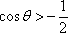

知识点
扫码查看完整答案与解析