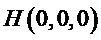- 平行关系的综合应用
- 共162题
17.如图,在三棱台





(Ⅰ)求证:
(Ⅱ)求二面角
正确答案
知识点
13.如图,在△ABC中,D是BC的中点,E,F是AD上的两个三等分点,



正确答案
知识点
16.如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且

求证:(1)直线DE∥平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
正确答案
(1)


又





⑵ 


且



又

又

又







知识点
11.平面a过正方体ABCD-A1B1C1D1的顶点A,a//平面CB1D1,

正确答案
知识点
现需要设计一个仓库,它由上下两部分组成,上部分的形状是正四棱锥




19.若

20.若正四棱锥的侧棱长为

正确答案

解析





故仓库的容积为
考查方向
解题思路
易错点
列函数解析式,求导与分类讨论。
正确答案

解析
设
则






当


当


因此,当

即
考查方向
解题思路
易错点
列函数解析式,求导与分类讨论。
11.圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16 + 20
正确答案
解析
由正视图和俯视图知,该几何体是半球与半个圆柱的组合体,圆柱的半径与球的半径都为r,圆柱的高为2r,其表面积为


考查方向
解题思路
由于三视图能有效的考查学生的空间想象能力,所以以三视图为载体的立体几何题基本上是高考每年必考内容,高考试题中三视图一般常与几何体的表面积与体积交汇.由三视图还原出原几何体,是解决此类问题的关键.
易错点
本题是三视图问题,主要是简单组合体,必须通过三视图看出直观图。
知识点
19.将边长为1的正方形








(1)求三棱锥
(2)求异面直线

正确答案
1,
2,
解析
知识点
如图,菱形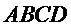
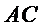
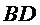
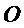
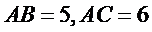
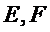
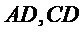
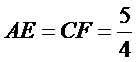
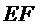
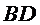
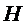
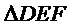
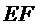
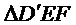
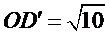
22.证明: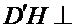
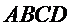
23.求二面角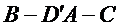

正确答案
(Ⅰ)详见解析;
解析
试题分析:本题属于立体几何的综合应用问题,属于中档题,只要掌握相关立体几何的知识,即可解决本题,解析如下:
⑴证明:∵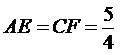
∴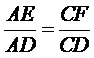
∴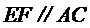
∵四边形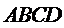
∴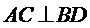
∴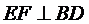
∴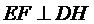
∴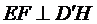
∵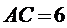
∴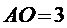
又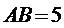
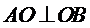
∴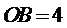
∴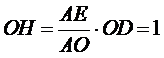
∴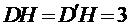
∴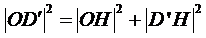
∴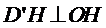
又∵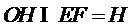
∴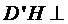
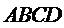
考查方向
解题思路
(1)先证明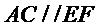
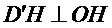
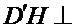
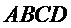
易错点
解题步骤不完整或考虑不全致推理片面导致出错。
正确答案
(Ⅱ)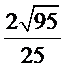
解析
试题分析:本题属于立体几何的综合应用问题,属于中档题,只要掌握相关立体几何的知识,即可解决本题,解析如下:
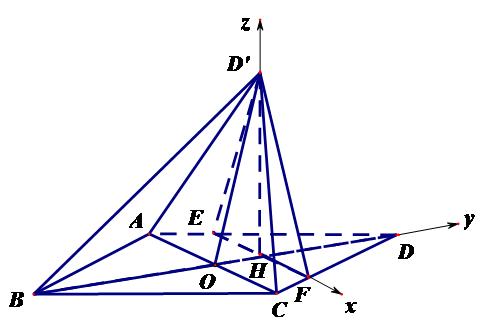
(II)如图,以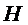
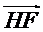
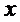
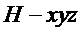
则
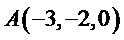
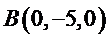
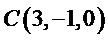
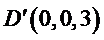
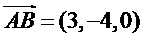
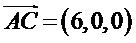
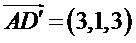
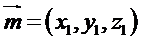
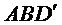
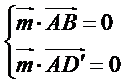
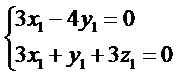
所以可以取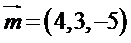
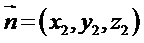
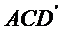
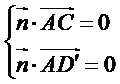
即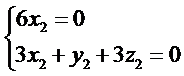
所以可以取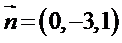
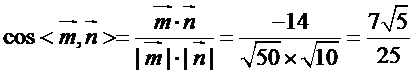
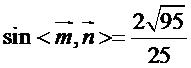
因此二面角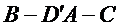
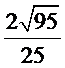
考查方向
解题思路
(2)建立空间直角坐标系,分别求出两个平面的法向量,再利用公式即可求出二面角.
易错点
解题步骤不完整或考虑不全致推理片面导致出错。
如图,在四棱柱





19. 求证:
20. 求二面角
21. 设E为棱


正确答案
(I)见解析;
解析
如图,以






(I)证明:依题意,可得


由此可得,



考查方向
解题思路
以



易错点
不会建坐标系去解答。
正确答案
(II) 
解析
(II)






设





因此有

所以二面角

考查方向
解题思路
(II)求出两个平面的法向量,可计算两个平面所成二面角的余弦值的大小,再求正弦值即可;
易错点
向量的坐标计算出现错误。
正确答案
(III) 
解析
(I








又因为

所以线段

考查方向
解题思路
(III) 设


易错点
坐标算错。
8.一个三棱锥的正视图和俯视图
正确答案
解析
选项A,B的情况结合正视图和俯视图都构不成三棱锥,C选项中有虚线部分,D选项中没有,结合实际情况,三棱锥不可能出现C中的情况,所以选D
考查方向
解题思路
先根据正视图和俯视图想象出侧视图的大致情况,然后根据选项判断
易错点
三视图还原成立体图错误
知识点
扫码查看完整答案与解析