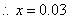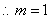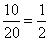- 频率分布直方图
- 共84题
空气质量指数

某市






(1)估计该城市一个月内空气质量类别为优的概率;
(2)从空气质量级别为三级和四级的数据中任取2个,
求恰好有一天空气质量类别为中度污染的概率。
正确答案
见解析。
解析
(1)由条形统计图可知,空气质量类别为优的天数为8天,
所以此次监测结果中空气质量类别为优的概率为
(2)样本中空气质量级别为三级的有4天,设其编号为
样本中空气质量级别为四级的有2天,设其编号为
则基本事件有:




其中恰好有1天空气质量类别为中度污染的情况为:

所以恰好有1天空气质量类别为中度污染的概率为
知识点
根据某固定测速点测得的某时段内过往的100辆机
动车的行驶速度(单位:km/h)绘制的频率分布直方图如
图(3)所示,该路段限速标志牌提示机动车辆正常行驶速
度为60 km/h~120 km/h,则该时段内过往的这100辆机
动车中属非正常行驶的有 辆,图中的x值为 。
正确答案
15、0.0175
解析
知识点
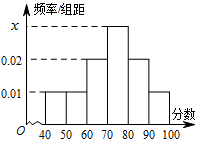
某学校对学生的考试成绩作抽样调查,得到成绩的频率分布直方图如图所示,其中[70,80)对应的数值被污损,记为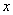
(1)求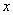
(2)记[90,100]为A组,[80,90)为B组,[70,80)为C组,用分层抽样的办法从[90,100],[80,90),[70,80)三个分数段的学生中抽出6人参加比赛,从中任选3人为正选队员,求正选队员中有A组学生的概率。
正确答案
见解析。
解析
(1)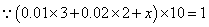
(2)设从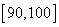
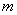
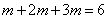
记从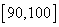
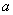
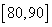
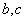
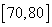
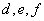
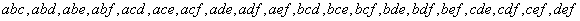
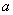
知识点
沙糖桔是柑桔类的名优品种,因其味甜如砂糖故名.某果农选取一片山地种植沙糖桔,收获时,该果农随机选取果树20株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间



(1)求

(2)从样本中产量在区间
上的果树至少有一株被抽中的概率.
正确答案
见解析。
解析
(1)解:样本中产量在区间

样本中产量在区间

依题意,有

根据频率分布直方图可知
解①②得:
(2)解:样本中产量在区间


产量在区间


从这



其中产量在


记“从样本中产量在区间

果树至少有一株被抽中”为事件

知识点
某班同学利用寒假在5个居民小区内选择两个小区逐户进行一次“低碳生活习惯”的调查,以计算每户的碳月排放量,若月排放量符合低碳标准的称为“低碳族”,否则称为“非低碳族”,若小区内有至少
(1)求所选的两个小区恰有一个为“非低碳小区”的概率;
(2)假定选择的“非低碳小区”为小区


正确答案
(1)
(2)三个月后小区
解析
(1)设三个“非低碳小区”为
用

则从5个小区中任选两个小区,所有可能的结果有10个,它们是









用

是:





故所求概率为
(2)由图1可知月碳排放量不超过
由图2可知,三个月后的低碳族的比例为
所以三个月后小区
知识点
为了解本市的交通状况,某校高一年级的同学分成了甲、乙、丙三个组,从下午13点到18点,分别对三个路口的机动车通行情况进行了实际调查,并绘制了频率分布直方图(如图),记甲、乙、丙三个组所调查数据的标准差分别为

正确答案
解析
略
知识点
如图,三行三列的方阵中有9个数

正确答案
解析
略
知识点
某小学对学生的身高进行抽样调查,如图,是将他们的身高(单位:厘米)数据绘制的频率分布直方图,由图中数据可知a= ▲ 。
正确答案
0.030
解析
略
知识点
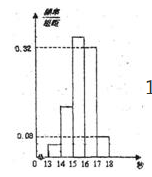
为了了解某年段1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);……;第五组[17,18],按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8.
(1)将频率当作概率,请估计该年段学生中百米成绩在[16,17)内的人数;
(2)求调查中随机抽取了多少个学生的百米成绩;
(3)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值
大于1秒的概率,
正确答案
见解析。
解析
(1)百米成绩在[16,17)内的频率为0.32×1=0.32. 0.32×1000=320
∴估计该年段学生中百米成绩在[16,17)内的人数为320人
(2)设图中从左到右前3个组的频率分别为3x,8x,19x依题意:得3x+8x+19x+0.32×1+0.08×1=1,
∴x=0.02
设调查中随机抽取了n个学生的百米成绩,则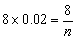
∴调查中随机抽取了50个学生的百米成绩.
(3)百米成绩在第一组的学生数有3×0.02×1×50=3,记他们的成绩为,a,b,c
百米成绩在第五组的学生数有0.08×1×50=4,记他们的成绩为m,n,p,q
则从第一、五组中随机取出两个成绩包含的基本事件有
{a,b},{a,c},{a,m},{a,n},{a,p},{a,q},{b,c},{b,m},{b,n},
{b,p},{b,q},{c,m},{c,n},{c,p},{c,q},{m,n},{m,p},{m,q},{n,p},{n,q},
{p,q}, 共21个
其中满足成绩的差的绝对值大于1秒所包含的基本事件有{a,b},{a,n},{a,p},{a,q},
{n,m},{b,n},{b,p},{b,q},{c,m},{c,n},{c,p},{c,q},共12个,
所以
知识点
如图是根据某城市部分居民2012年月平均用水量(单位:吨)绘制的样本频率分布直方图,样本数据的分组为[1,2),[2,3),[3,4),……,[6,7],已知样本中月均用水量低于4吨的户数为102,则样本中月均用水量不低于4吨的户数为
正确答案
解析
略
知识点
扫码查看完整答案与解析