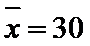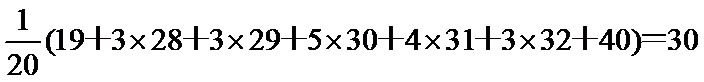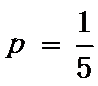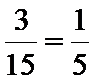- 相互独立事件的概率乘法公式
- 共42题
某车间20名工人年龄数据如下表:
21.求这20名工人年龄的众数与平均数;
22.以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
23.从年龄在24和26的工人中随机抽取2人,求这2人均是24岁的概率。
正确答案
众数是30;
解析
(Ⅰ) 由题意可知,这20名工人年龄的众数是30,
这20名工人年龄的平均数为
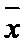
考查方向
解题思路
根据众数和平均数的定义,即可得出;
易错点
熟记众数和平均数的概念.
正确答案
见解析
解析
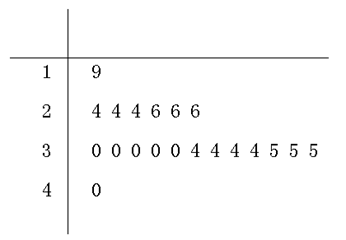
这20名工人年龄的茎叶图如图所示:
考查方向
解题思路
根据画茎叶图的步骤,画图即可;
易错点
无
正确答案
解析
记年龄为24岁的三个人为A1,A2,A3;年龄为26岁的三个人为B1,B2,B3则从这6人中随机抽取2人的所有可能为
{A1,A2},{A1,A3},{A2,A3},{A1,B1},{A1,B2},
{A1,B3},{A2,B1},{A2,B2},{A2,B,3},{A3,B1},
{A3,B2},{A,3,B3},{B1,B2},{B1,B3},{B2,B3}共15种。
满足题意的有{A1,A2},{A1,A3},{A2,A3}3种,
故所求的概率为P=
考查方向
解题思路
利用枚举法,将6人中随机抽取2人的所有可能的情况列举出来,再求概率.
易错点
古典概型中使用枚举时,要注意不重不漏.
某车间20名工人年龄数据如下表:
21.求这20名工人年龄的众数与平均数;
22.以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
23.从年龄在24和26的工人中随机抽取2人,求这2人均是24岁的概率。
正确答案
众数是30;
解析
(Ⅰ) 由题意可知,这20名工人年龄的众数是30,
这20名工人年龄的平均数为

考查方向
解题思路
根据众数和平均数的定义,即可得出;
易错点
熟记众数和平均数的概念.
正确答案
见解析
解析
这20名工人年龄的茎叶图如图所示:
考查方向
解题思路
根据画茎叶图的步骤,画图即可;
易错点
无
正确答案
解析
记年龄为24岁的三个人为A1,A2,A3;年龄为26岁的三个人为B1,B2,B3则从这6人中随机抽取2人的所有可能为
{A1,A2},{A1,A3},{A2,A3},{A1,B1},{A1,B2},
{A1,B3},{A2,B1},{A2,B2},{A2,B,3},{A3,B1},
{A3,B2},{A,3,B3},{B1,B2},{B1,B3},{B2,B3}共15种。
满足题意的有{A1,A2},{A1,A3},{A2,A3}3种,
故所求的概率为P=
考查方向
解题思路
利用枚举法,将6人中随机抽取2人的所有可能的情况列举出来,再求概率.
易错点
古典概型中使用枚举时,要注意不重不漏.
正确答案
LUE
知识点
正确答案
略
知识点
23.已知构成某系统的元件能正常工作的概率为p(0<p<1),且各个元件能否正常工作是相互独立的。今有2n(n大于1)个元件可按下图所示的两种联结方式分别构成两个系统甲、乙。
(1)试分别求出系统甲、乙能正常工作的概率p1,p2;
(2)比较p1与p2的大小,并从概率意义上评价两系统的优劣。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
正确答案
知识点
19.设某校新、老校区之间开车单程所需时间为


(1)求

(2)刘教授驾车从老校区出发,前往新校区做一个50分钟的讲座,结束后立即返回老校区,求刘教授从离开老校区到返回老校区共用时间不超过120分钟的概率.
正确答案
19.(1)由统计结果可得T的频率分步为
以频率估计概率得T的分布列为
从而 
(2)设

解法一:

解法二:
故
解析
解析已在路上飞奔,马上就到!
知识点
18.(本题满分12分)
某公司为了解用户对其产品的满意度,从

A地区:62 73 81 92 95 85 74 64 53 76
78 86 95 66 97 78 88 82 76 89
B地区:73 83 62 51 91 46 53 73 64 82
93 48 65 81 74 56 54 76 65 79
(Ⅰ)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,得出结论即可);
(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个等级:
记时间C:“A地区用户的满意度等级高于B地区用户的满意度等级”.假设两地区用户的评价结果相互独立.根据所给数据,以事件发生的频率作为相应事件发生的概率,求C的概率.
正确答案
(Ⅰ)详见解析;(Ⅱ)
试题分析:(Ⅰ)将
(Ⅱ)事件“A地区用户的满意度等级高于B地区用户的满意度等级”分为两种情况:当B地区满意度等级为不满意时,A地区的满意度等级为满意或非常满意;当B地区满意度等级为满意时,A地区满意度等级为非常满意.再利用互斥事件和独立事件的概率来求解.
试题(Ⅰ)两地区用户满意度评分的茎叶图如下

则







由所给数据得












解析
解析已在路上飞奔,马上就到!
知识点
20.某厂用鲜牛奶在某台设备上生产





该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利
(1)求
(2) 若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10000元的概率.
正确答案
20.(1)设每天



目标函数为 
当

将

当



最大获利
当

将

当



最大获利
当
四个顶点分别为
将

当



最大获利
故最大获利
因此,
(2)由(1)知,一天最大获利超过10000元的概率
由二项分布,3天中至少有1天最大获利超过10000元的概率为
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析