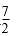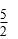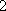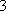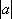- n次独立重复试验中恰好发生k次的概率
- 共66题
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
已知抛物线C：y2＝8x的焦点为F，准线为l，P是l上一点，Q是直线PF与C的一个交点，若＝4，则|QF|＝( )
A
B3
C
D2
正确答案
解析
由题知F(2，0)，设P(－2，t)，Q(x0，y0)，则FP＝(－4，t)，＝(x0－2，y0)，由FP＝4FQ，得－4＝4(x0－2)，解得x0＝1，根据抛物线定义得|QF|＝x0＋2＝3.
知识点
设
正确答案
解析
“
“
知识点
抛物线x2＝2py（p>0）的焦点为F，其准线与双曲线
正确答案
6
解析
抛物线的准线方程为
知识点
已知离散型随机变量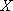
则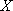
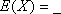
A
B
C
D
正确答案
解析
A；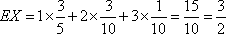
知识点
如图，从A1(1,0,0)，A2(2,0,0)，B1(0,1,0)，B2(0,2,0)，C1(0,0,1)，C2(0,0,2)这6个点中随机选取3个点，将这3个点及原点O两两相连构成一个“立体”，记该“立体”的体积为随机变量V(如果选取的3个点与原点在同一个平面内，此时“立体”的体积V＝0)。
（1）求V＝0的概率；
（2）求V的分布列及数学期望EV.
正确答案
见解析
解析
（1）从6个点中随机选取3个点总共有
（2）V的所有可能取值为0，
由V的分布列可得
知识点
已知a>0，则x0满足关于x的方程ax=6的充要条件是
A
B
C
D
正确答案
解析
由于a>0,令函数
知识点
（坐标系与参数方程选做题）若以直角坐标系的原点为极点，
A
B
C
D
正确答案
解析
根据直角坐标和极坐标的互化公式x=ρcosθ，y=ρsinθ，y=1﹣x（0≤x≤1），
可得ρcosθ+ρsinθ=1，即 ρ=
知识点
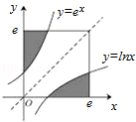
如图，在边长为e（e为自然对数的底数）的正方形中随机撒一粒黄豆，则它落到阴影部分的概率为 。
正确答案
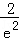
解析
综合题；概率与统计。
利用定积分计算阴影部分的面积，利用几何概型的概率公式求出概率。
由题意，y=lnx与y=ex关于y=x对称，
∴阴影部分的面积为2
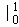
∵边长为e（e为自然对数的底数）的正方形的面积为e2，
∴落到阴影部分的概率为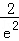
知识点
已知平面向量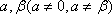
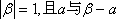
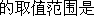
正确答案
解析
利用题设条件及其几何意义表示在三角形中，即可迎刃而解，设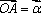
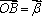
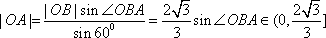
知识点
扫码查看完整答案与解析