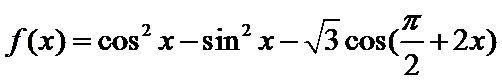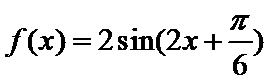- 正弦函数的单调性
- 共119题
9.定义在区间[0,3π]上的函数y=sin2x的图象与y=cosx的图象的交点个数是 .
正确答案
7
知识点
15.已知函数f(x)=4tanxsin(


(Ⅰ)求f(x)的定义域与最小正周期;
(Ⅱ)讨论f(x)在区间[
正确答案




所以, 
解析



由
设

所以, 当



知识点
7.定义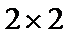
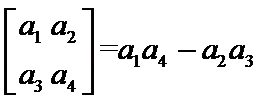
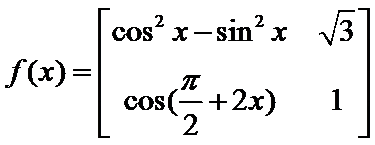
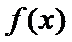
正确答案
解析
根据矩阵的定义,可以得到
所以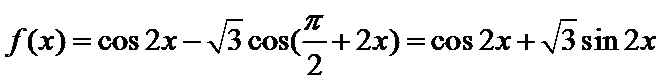
根据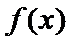
考查方向
三角函数
解题思路
先根据矩阵的定义,得到f(x)的解析式,然后根据函数的解析式判断函数的相关性质.
易错点
三角函数公式记忆混淆
知识点
6.已知


正确答案
解析
由









考查方向
解题思路
1、先由


2、然后求函数


易错点
1、将三角函数的最值以极值的形式出现导致无法理解题意致误。
2、将三角函数的最值、单调区间记错、求错出错。
知识点
8.设函数


正确答案
解析
由题得周期为




考查方向
解题思路
该题首先根据周期求出

易错点
本题易错在(1)忽略A为负值(2)对称中心计算错误(3)单调性不能判断
知识点
16.已知函数


(I)求
(II)在




正确答案
解:(Ⅰ)因为

所以

解
得:
所以函数
(Ⅱ) 因为
得
因为

所以

所以
根据正弦函数的图象可以看出,

此时

所以
解析
见答案
考查方向
本题主要考查正弦定理和余弦定理的性质,属于基础题
解题思路
根据题意换成三角函数一般形式,然后根据函数最值判断,第二问求出ABC角度的大小进而判定三角形形状。
易错点
混淆两个定理的性质
知识点
6.函数f(x)=


正确答案
解析
由题意可知函数在x=
所以
考查方向
本题考查了函数的图象及单调性,最值等性质。
解题思路
利用函数

易错点
看不出函数在x=
知识点
15.已知函数

(Ⅰ)求
(Ⅱ)设


正确答案
(Ⅰ)



解析
试题分析:本题属于三角函数的基本问题,题目的难度是逐渐由易到难,(1)直接按步骤来求,(2)要注意三角恒等变换的正确性;
(Ⅰ)解:

所以函数

由

得
所以函数


(注:或者写成单调递增区间为

(Ⅱ)解:由题意,得
因为函数

所以

所以

解得

又因为
所以

考查方向
本题主要考查了三角恒等变换以及三角函数的图象与性质,三角函数的性质的考查主要分以下几类:
1.三角函数的定义域,
2.三角函数的单调性与最值,
3.三角函数的周期性,
4.三角函数的奇偶性或对称性.
解题思路
本题考查三角恒等变换、三角函数的图象与性质,解题步骤如下:1.利用二倍角公式和配角公式将函数




易错点
1、第一问中的单调递增区间易错误写成集合的形式,或丢掉“
2、第二问中易利用

知识点
16.已知函数

(Ⅰ)求函数
(Ⅱ)若

正确答案
(Ⅰ)函数
(Ⅱ)

解析
本题第二问特别要注意:一定要结合函数的定义域正确书写增区间.

所以函数

(Ⅱ)解:由

得
所以函数


所以当



(注:或者写成增区间为

考查方向
解题思路
本题主要考查正、余弦的二倍角公式及
1、把

2、由

3、最后通过
易错点
本题体现了三角函数部分的基本的解题思想方法,为学生非常熟悉的题型对于第二问可能由于思维定势审题不全忽略

知识点
(本小题满分13分)
已知函数

(Ⅰ)若


(Ⅱ)若



正确答案
考查方向
易错点
1、本题在第一问
知识点
扫码查看完整答案与解析