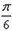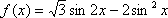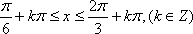- 正弦函数的单调性
- 共119题
已知函数
(1)求f(x)的最小正周期;
(2)设
正确答案
见解析。
解析
知识点
设
(1)求
(2)△ABC中锐角




正确答案
见解析。
解析
(1)

故


(2)由

故

故


∴
知识点
若m是一个给定的正整数,如果两个整数a、b用m除所得的余数相同,则称a与b对m校同余,记作

正确答案
解析
:由题意,22012=4×8670=4×(7+1)670=4×[C


∴22012≡4(mod7),
若22012≡r[mod(7)],则r可能为4。
故选B,
知识点
设



(1) 求证: 
(2)若

正确答案
见解析
解析
解: (1)因为

(2)因为
所以
又由

所以
由(1),得
知识点
设函数
(1)写出函数f(x)的最小正周期及单调递减区间;
(2)当

正确答案
见解析。
解析
(1)

故函数f(x)的单调递减区间是
(2)∵


当


知识点
已知 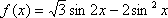
(1)求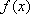
(2)若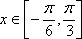
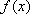

正确答案
(1)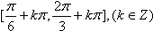
解析
(1)因为
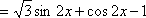
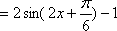
所以,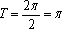
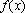

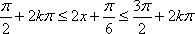
所以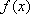
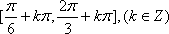
(2)因为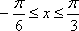
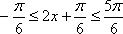
所以有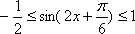
由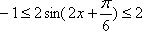
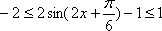
所以,函数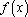
此时,因为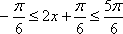
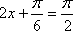
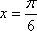
知识点
已知函数

(1)求函数
(2)若

正确答案
(1)

(2)
解析
(1)由题设
由

故函数


(2)由

考察函数

于是
故

知识点
已知

(1)若

(2)若函数y=f(x)的定义域为[
正确答案
(1)
解析
(1)f(x)=-2asin2x+2asinxcosx+a+b=2asin+b,
∵a>0,∴由2kπ-≤2x+≤2kπ+得, kπ-≤x≤kπ+,k∈Z。
∴函数y=f(x)的单调递增区间是[kπ-,kπ+](k∈Z)
(2)x∈[,π]时,2x+∈[,], sin∈[-1,]
当a>0时,f(x)∈[-2a+b,a+b]
当a<0时,f(x)∈[a+b,-2a+b]
综上知,
知识点
设函数



(1)求
(2)在








正确答案
见解析
解析
(1)

令

(2)由


∵
又∵

∴在

由

知识点
设函数



(1)求
(2)在








正确答案
见解析
解析
(1)

令

(2)由


∵
又∵

∴在

由

知识点
扫码查看完整答案与解析