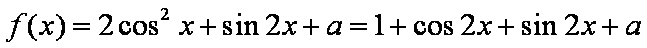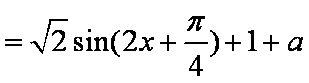- 正弦函数的单调性
- 共119题
已知椭圆C: 
(1)求椭圆C的方程;
(2)若斜率为k的直线过点M(2,0),且与椭圆C相交于A,B两点.试探讨k为何值时,三角形OAB为直角三角形.
正确答案
见解析
解析
(1)
所以椭圆方程为
(2)由已知直线AB的斜率存在,设AB的方程为:
由
,得:

设
(1)若






(2)若





解得,



知识点
已知函数
(1)求函数
(2)若存在


(3)对任意的


正确答案
见解析
解析
(1)

函数

(2)当

(理)存在


(3)存在唯一的

(文理)当


设

得
所以
∵
∴



知识点
设函数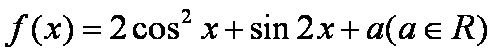
(1)求函数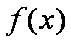
(2)当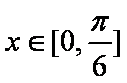
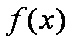
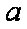
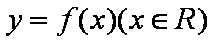
正确答案
见解析
解析
解:(1)
则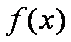
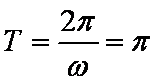
且当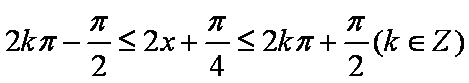
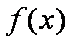
即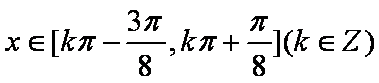
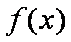
(2)当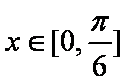
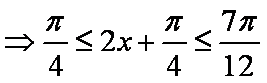
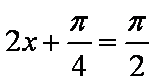
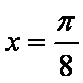
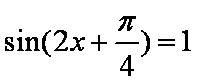
所以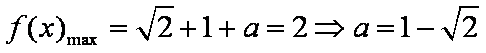
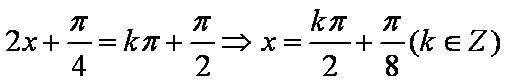
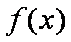
知识点
已知函数




(1)求函数
(2)把函数


正确答案
见解析
解析
解:(1)


依题意:











(2)把函数



平移后的图象对应的函数解析式为:
知识点
已知数列


(1)求数列
(2) 若
正确答案
见解析
解析
(1)由题设






(2)由(1)数列




记


=

当












知识点
扫码查看完整答案与解析