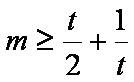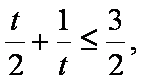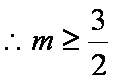- 空间点、线、面的位置关系
- 共375题
如图,在直三棱柱








(1)求证:
(2)求二面角
正确答案
见解析。
解析
(1)连接

∵



面

∴



∴



∴

(2)∵在直三棱柱

∴
以



由(1)知

∴点




设平面

∵

∴


同理,平面

设二面角

则
∴
知识点
在如图所示的几何体中,面






(1)求证:

(2)线段



正确答案
见解析
解析
解析:(1)证明:因为
在△
所以
又因为
所以

(2)
线段



证明如下:
因为


因为


所以

在等腰梯形

设

所以

设平面

所以


假设线段



设平面

所以


要使平面


即 
所以线段



知识点
某音乐喷泉喷射的水珠呈抛物线形,它在每分钟内随时间(秒)的变化规律大致可用




(1)试求此喷泉喷射的圆形范围的半径最大值;
(2)若在一建筑物前计划修建一个矩形花坛并在花坛内装置两个这样的喷泉,则如何设计花坛的尺寸和两个喷水器的位置,才能使花坛的面积最大且能全部喷到水?
正确答案
见解析
解析
(1)当
因


从而当


所以此喷泉喷射的圆形范围的半径最大值是
(2)设花坛的长、宽分别为xm,ym,根据要求,矩形花坛应在喷水区域内,顶点应恰好位于喷水区域的边界,依题意得:

问题转化为在


法一:





法二:∵


∴当




答:花坛的长为

知识点
如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上。
(1)设AD=x(x
(2)如果DE是灌溉水管,为节约成本,希望它最短,DE的位置应在哪里?如果DE是参观线路,则希望它最长,DE的位置又应在哪里?请给予证明。
正确答案
见解析
解析
(1)在△ADE中,由余弦定理得:

又
把代入得
∴
∵ 
即函数的定义域为
(2)如果DE是水管,则
当且仅当


如果DE是参观线路,记
∴函数


故
∴
即DE为AB中线或AC中线时,DE最长.…………………………………………… 12分
知识点
已知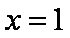
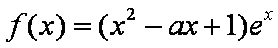
(1)求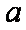
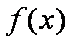
(2)若对于任意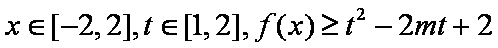
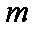
正确答案
见解析。
解析
(1)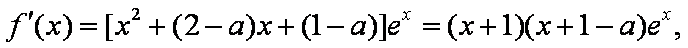
由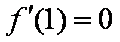
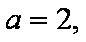
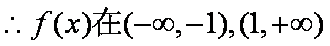
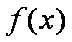
(2)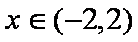
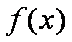
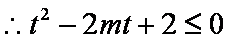
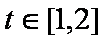
易知: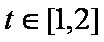
知识点
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°。
(1)求证:BD⊥平面PAC;
(2)若PA=AB,求PB与AC所成角的余弦值;
(3)当平面PBC与平面PDC垂直时,求PA的长。
正确答案
见解析
解析
(1)证明:因为四边形ABCD是菱形, 所以AC⊥BD。
又因为PA⊥平面ABCD, 所以PA⊥BD,
所以BD⊥平面PAC。
(2)设AC∩BD=O。 因为∠BAD=60°,PA=AB=2, 所以BO=1,AO=CO=
如图,以O为坐标原点,OB、OC所

P(0,-


所以=(1,

设PB与AC所成角为θ,则

(3)由(2)知=(-1,
设P(0,-

设平面PBC的法向量m=(x,y,z), 则·m=0,·m=0。
所以 



同理,可求得平面PDC的法向量n=
因为平面PBC⊥平面PDC, 所以m·n=0,即-6+

所以当平面PBC与平面PDC垂直时,PA=
知识点
持续性的雾霾天气严重威胁着人们的身体健康,汽车的尾气排放是造成雾霾天气的重要因素之一.为此,某城市实施了机动车尾号限行,该市报社调查组为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
(1)请估计该市公众对“车辆限行”的赞成率和被调查者的年龄平均值;
(2)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行追踪调查,记被选4人中不赞成“车辆限行”的人数为

(3)若在这50名被调查者中随机发出20份的调查问卷,记


正确答案
见解析
解析
本小题主要考查样本频率分布、随机变量的分布列、数学期望等基础知识,考查数据处理能力、运算求解能力以及应用用意识,考查必然与或然思想等。
(1)该市公众对“车辆限行”的赞成率约为:
被调查者年龄的平均约为:
(2)依题意得:

所以
所以

(3)


当


当


即

故有:

知识点
21.已知双曲线
(1)求双曲线的方程;
(2)已知直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 如图1所示 :在边长为













(I)在底边






(II)求直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点。
(1)求证:AF⊥CD;
(2)求直线AC与平面CBE所成角的大小的余弦值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析