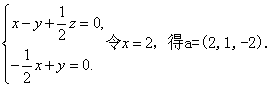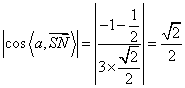- 空间点、线、面的位置关系
- 共375题
如图,在直三棱柱









(1)求异面直线

(2)求点

正确答案
(1)
解析
(1)设







连接ME,在
所以异面直线


(2)

以点






设平面
则
所以平面

又
所以点


知识点
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=900。
(1)求证:PC⊥BC;
(2)求点A到平面PBC的距离。
正确答案
见解析。
解析
(1)证明:因为PD⊥平面ABCD,BC
由∠BCD=900,得CD⊥BC,
又PD

所以BC⊥平面PCD。
因为PC
(2)
(方法一)分别取AB、PC的中点E、F,连DE、DF,则:
易证DE∥CB,DE∥平面PBC,点D、E到平面PBC的距离相等。
又点A到平面PBC的距离等于E到平面PBC的距离的2倍。
由(1)知:BC⊥平面PCD,所以平面PBC⊥平面PCD于PC,
因为PD=DC,PF=FC,所以DF⊥PC,所以DF⊥平面PBC于F。
易知DF=

(方法二)体积法:连结AC。设点A到平面PBC的距离为h。
因为AB∥DC,∠BCD=900,所以∠ABC=900。
从而AB=2,BC=1,得

由PD⊥平面ABCD及PD=1,得三棱锥P-ABC的体积
因为PD⊥平面ABCD,DC
又PD=DC=1,所以
由PC⊥BC,BC=1,得

由


故点A到平面PBC的距离等于
知识点
在长为12cm的线段AB上任取一点C.现作一矩形,领边长分别等于线段AC,CB的长,则该矩形面积小于32cm2的概率为
正确答案
解析
设线段AC的长为


由



知识点
已知曲线C1的参数方程为



(1)把C1的参数方程化为极坐标方程;
(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π)。
正确答案
(1) 

解析
将


即




∴

(2)

由





知识点
如图,在直三棱柱






(1)求证:

(2)若二面角


正确答案
见解析
解析
解析:(1)过点





∵面



∴直线

又∵面



∴




又易知



又点

所以

(2)延长




过




由此知

设
在

在

在

据题意有:

所以
知识点
如图,在三棱锥









求证:(1)平面

(2)
正确答案
见解析。
解析
证明:(1)∵

∵E.F分别是SA.SB的中点 ∴EF∥AB
又∵EF

同理:FG∥平面ABC
又∵EF


(2)∵平面




∴AF⊥平面SBC 又∵BC
又∵



知识点
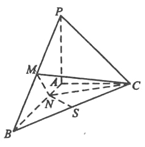
已知三棱锥P-ABC中,PA⊥ABC,AB⊥AC,PA=AC=½AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点。
(1)证明:CM⊥SN;
(2)求SN与平面CMN所成角的大小。
正确答案
见解析。
解析
设PA=1,以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立空间直角坐标系如图。
则P(0,0,1),C(0,1,0),B(2,0,0),M(1,0,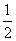
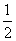
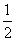
(1)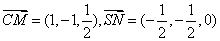
因为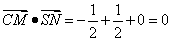
所以CM⊥SN
(2)
设a=(x,y,z)为平面CMN的一个法向量,
则
因为
所以SN与片面CMN所成角为45°。
知识点
已知函数f(x)=x3+ax2+bx+c,下列结论中错误的是( )。
正确答案
解析
∵x0是f(x)的极小值点,则y=f(x)的图像大致如下图所示,则在(-∞,x0)上不单调,故C不正确。
知识点
将一个质点随机投放在关于


正确答案
解析
略
知识点
9.某班班会准备从含甲、乙、丙的7名学生中选取4人发言,要求甲、乙两人至少有一个参加,若甲、乙同时参加时丙不能参加,且甲、乙两人的发言顺序不能相邻,那么不同的发言顺序有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析