空间点、线、面的位置关系
共375题

空间点、线、面的位置关系
共375题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 13 分

如图所示，在多面体，四边形，均为正方形，为的中点，过的平面交于F.

21.证明：

22.求二面角余弦值.

第(1)小题正确答案及相关解析

正确答案

解析

（Ⅰ）证明：由正方形的性质可知，且，所以四边形为平行四边形，从而，又面，面，于是面，又面，而面面，所以.

解题思路

（Ⅰ）证明：依据正方形的性质可知，且，，从而为平行四边形，则，根据线面平行的判定定理知面，再由线面平行的性质定理知.

易错点

找不到线面平行和线线平行的关系。

第(2)小题正确答案及相关解析

正确答案

（2）

解析

（Ⅱ）因为四边形，，均为正方形，所以，且，以为原点，分别以为轴，轴，轴单位正向量建立，如图所示的空间直角坐标系，可得点的坐标.而点为的中点，所以点的坐标为.

设面的法向量.而该面上向量，由得应满足的方程组，为其一组解，所以可取.设面的法向量，而该面上向量，由此同理可得.所以结合图形知二面角的余弦值为.

考查方向

1.线面平行的判定定理与性质定理；2.二面角的求解.

解题思路

因为四边形，，均为正方形，所以，且，可以建以为原点，分别以为轴，轴，轴单位正向量的平面直角坐标系，写出相关的点的坐标，设出面的法向量.由得应满足的方程组，为其一组解，所以可取.同理的法向量.所以结合图形知二面角的余弦值为.

易错点

找不到二面角的平面角,计算能力弱.

题型：填空题

填空题 · 4 分

16．在平行六面体的一个面所在的平面内，任意画一条直线，则与它异面的平行六面体的棱的条数可能是____________（填上所有可能结果）。

正确答案

4或6或7或8

解析

解析已在路上飞奔，马上就到！

知识点

异面直线的判定排列、组合及简单计数问题

题型：单选题

单选题 · 5 分

9.从正方体的棱和各个面的面对角线中选出条，使得其中任意两条线段所在的直线都是异面直线，则的最大值是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

异面直线的判定排列、组合及简单计数问题

题型：填空题

填空题 · 4 分

5．在的取值范围为_______

正确答案

（1，3）

解析

解析已在路上飞奔，马上就到！

知识点

异面直线的判定

题型：简答题

简答题 · 12 分

如图，高为3的直三棱柱中，底面是直三角形，，为的中点，在线段上，，且．

22.求证：平面；

23.求平面与平面所成的锐角二面角的余弦值．

第(1)小题正确答案及相关解析

正确答案

详见解析

考查方向

直线与平面垂直的判定

第(2)小题正确答案及相关解析

正确答案

略

题型：单选题

单选题 · 5 分

过正方体的顶点A作直线L，使L与棱,,所成的角都相等，这样的直线L可以作

A1条

B2条

C3条

D4条

正确答案

解析

考查空间感和线线夹角的计算和判断，重点考查学生分类、划归转化的能力。第一类：通过点A位于三条棱之间的直线有一条体对角线AC1，第二类：在图形外部和每条棱的外角和另2条棱夹角相等，有3条，合计4条。

知识点

异面直线及其所成的角空间中直线与直线之间的位置关系

题型：简答题

简答题 · 10 分

如图，平面平面ABC，是等腰直角三角形，AC =BC= 4，四边形ABDE是直角梯形，BD∥AE，BD BA，,，

求直线CD和平面ODM所成角的正弦值。

正确答案

见解析。

解析

∵，又∵面面，面面，，

∴，∵BD∥AE，∴，

如图所示，以C为原点，分别以CA，CB为x，y轴，以过点C且与平面ABC垂直的直线为z轴，建立空间直角坐标系，

∵，

∴设各点坐标为，，，

，，

则，，，

，，

设平面ODM的法向量，则由

且可得

令，则，，∴，

设直线CD和平面ODM所成角为，则

，

∴直线CD和平面ODM所成角的正弦值为，

知识点

异面直线的判定

题型：简答题

简答题 · 12 分

如图，在斜三棱柱中，点、分别是、的中点，平面.已知，.

（1）证明：平面；

（2）求异面直线与所成的角；

（3）求与平面所成角的正弦值。

正确答案

见解析

解析

解法一：（1）证明：∵点、分别是、的中点，

∴ ，又∵平面，平面，

∴平面。

（2）∵平面，∴，又∵，且，

∴平面,∴。·

又∵， ∴四边形为菱形，

∴，且∴平面,

∴，即异面直线与所成的角为。

（3）设点到平面的距离为，∵，

即△。

又∵在△中，

,∴△。

∴，∴与平面所成角的正弦值

解法二：如图建系，，，，，。

（1）∵，，∴，即，

又∵平面，平面，∴平面。

（2）∵，，∴，即∴，

∴异面直线与所成的角为。

（3）设与平面所成角为，∵，

设平面的一个法向量是

则即

不妨令，可得，·

∴，

∴与平面所成角的正弦值。·

知识点

异面直线的判定

题型：填空题

填空题 · 3 分

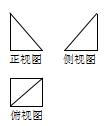
12．一个几何体的三视图如图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，若要拼成一个棱长为1的正方体，则需要这样的几何体（）个。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

异面直线的判定

题型：简答题

简答题 · 12 分

19．如图，某人打算做一个正四棱锥形的金字塔模型，先用木料搭边框，再用其他材料填充。已知金字塔的每一条棱和边都相等。

（1）求证：直线垂直于直线；

（2）若搭边框共使用木料24米，则需要多少立方米的填充材料才能将整个金字塔内部填满？

正确答案

（1）略；

（2）；

解析

（1）如图，连接交于点，则为线段中点，

在正方形中，对角线

在中，，

，平面

（2）边长为3米

解直角三角形SOB，得棱锥的高

立方米

答：需要立方米填充材料.

考查方向

本题考查了空间直线与平面的位置关系，棱锥体积的计算。

解题思路

1、空间关系的判断与证明通常需要直线与直线，直线与平面，平面与平面三种关系相互转换，本题可以先把线线关系转化为线面关系，再转为线线关系求证。

2、解决正棱锥有关问题通常要研究底边，侧棱，高，斜高，底面外接圆半径，内切圆半径组成的四个直角三角形。本题可以由侧棱，底面外接圆半径和高组成的直角三角形入手求解。

易错点

注意搭建正四棱锥不仅有四条侧棱，含有四条底边。

知识点

棱柱、棱锥、棱台的体积异面直线的判定

继续学习学习下一知识点

下一知识点 : 直线、平面平行的判定与性质

百度题库 > 高考 > 理科数学 > 空间点、线、面的位置关系

扫码查看完整答案与解析