- 空间点、线、面的位置关系
- 共375题
11.平面a过正方体ABCD-A1B1C1D1的顶点A,a//平面CB1D1,

正确答案
知识点
17.如图,在四棱锥P-ABCD中,平面PAD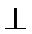
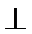
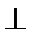
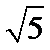
(I)求证:PD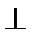
(II)求直线PB与平面PCD所成角的正弦值;
(III)在棱PA上是否存在点M,使得BM//平面PCD?若存在,求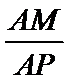
正确答案
知识点
14.α、β是两个平面,m、n是两条直线,有下列四个命题:
①如果m⊥n,m⊥α,n∥β,那么α⊥β.
②如果m⊥α,n∥α,那么m⊥n.
③如果α∥β,m
④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.
其中正确的命题有 .(填写所有正确命题的编号)
正确答案
②③④
知识点
α、β是两个平面,m、n是两条直线,有下列四个命题:
①如果m⊥n,m⊥α,n∥β,那么α⊥β.
②如果m⊥α,n∥α,那么m⊥n.
③如果α∥β,m
④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.
其中正确的命题有 .(填写所有正确命题的编号)
正确答案
②③④
知识点
在四棱锥






21.证明:
22.在线段



正确答案
见解析
解析
试题分析:本题属于立体几何的综合应用问题,属于中档题,只要掌握相关立体几何的知识,即可解决本题,解析如下:
由PA⊥平面ABCD,得DE⊥PA.连接AE,因为
考查方向
解题思路
利用相关定理进行证明.
易错点
相关定理不熟容易处错。
正确答案
见解析
解析
试题分析:本题属于立体几何的综合应用问题,属于中档题,只要掌握相关立体几何的知识,即可解决本题,解析如下:过点F作FH∥ED交AD于点H,则FH∥平面PED,且有AH=

由面面平行的判定定理可得平面GEH∥平面PFD.,进而由面面平行的性质得到EG∥平面PFD,从而确定G点位置.
考查方向
解题思路
假设平行,利用平行确定点的位置.
易错点
相关定理不熟容易处错。
4.设a,l是直线,α和β是平面,则下列说法正确的是( )
正确答案
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是简单。
考查方向
本题主要考查了线面位置关系,在近几年的各省高考题出现的频率较高。
解题思路
本题考查线面位置关系,解题步骤如下:
由题可知,A中可能l∥β;B中可能l在β内;C中可能α⊥β。
易错点
本题易在判断线是否在面上发生错误。
知识点
扫码查看完整答案与解析