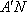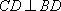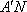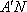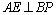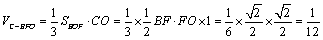- 棱柱、棱锥、棱台的体积
- 共170题
如图,几何体








(1)求异面直线

(2)求几何体
正确答案
见解析
解析
(1)解法一:在



由题意得,



∴




∵ 

∴
∴
则

所成的角.
由平面几何知识及勾股定理可以得
在

∵ 异面直线的夹角范围为
∴ 异面直线


解法二:
同解法一得


分别为
可得
∴ 
得
设向量


∵ 异面直线的夹角范围为
∴ 异面直线


(2)
如图,连结





∵

∴ 几何体
知识点
在直角梯形ABCD中,ADBC,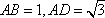
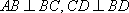
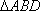
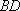
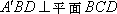
(1)求证: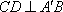
(2)求三棱锥
(3)在线段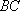
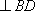
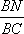
正确答案
见解析。
解析
(1)∵平面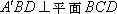
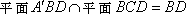
∴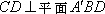
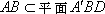
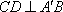
(2)如图(1)在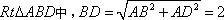
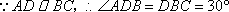
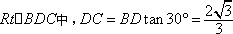
∴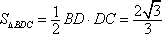
如图(2),在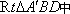
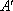

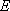
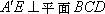
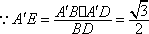
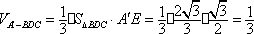
(3)在线段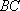
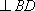
如图(2)在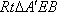
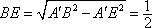
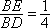
过点E做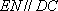
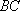
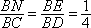
∵
又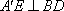
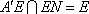
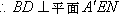
又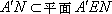
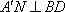
∴在线段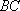
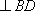
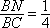
知识点
如图,已知





的中点。
(1)求证:

(2)求证:平面BCE⊥平面
(3)求此多面体的体积
正确答案
见解析。
解析
(1)取CE中点P,连结FP、BP,∵F为CD的中点, ∴FP∥DE,且FP=
又AB∥DE,且AB=
∴ABPF为平行四边形,∴AF∥BP,
又∵AF

(2)∵
∵AB⊥平面ACD,DE//A

∴DE⊥AF 又AF⊥CD,CD∩DE=D
∴AF⊥平面
又∵BP
(3)此多面体是一个以C为定点,以四边形ABED为底边的四棱锥,


知识点
在长方体






(1)求异面直线
(2)求以
正确答案
(1)
解析
联结


又

∴

由

∴


(2)由题意可知,点


∴
∵
∴
知识点
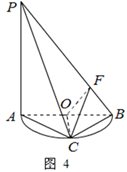
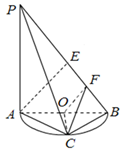
图4,PA垂直于⊙O所在平面ABC,AB为⊙O的直径,PA=AB=2,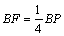
(1)证明:BC平面PAC;
(2)证明:CFBP;
(3)求四棱锥C—AOFP的体积.
正确答案
见解析。
解析
(1)
证明:∵PA⊥平面ABC,BC⊥平面ABC,
∴BC⊥PA.
∵△ACB是直径所对的圆周角,
∴
又∵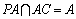
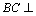
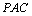
(2)证明:∵PA⊥平面ABC,OC⊥平面ABC,
∴OC⊥PA.
∵C是弧AB的中点,
∴△ABC是等腰三角形,AC=BC,
又O是AB的中点,∴OC⊥AB.
又∵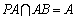
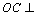
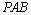
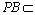
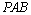
∴
设BP的中点为E,连结AE,则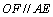
∴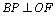
∵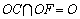
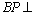
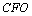
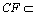
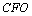
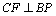
(3)解:由(2)知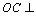
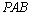
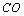

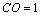
又∵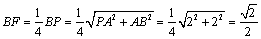
∴
又∵
∴四棱锥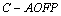
知识点
扫码查看完整答案与解析