· 空间几何体的三视图、表面积和体积

· 棱柱、棱锥、棱台的体积

棱柱、棱锥、棱台的体积
共170题

· 空间几何体的三视图、表面积和体积

· 棱柱、棱锥、棱台的体积

棱柱、棱锥、棱台的体积
共170题

热门试卷

X 查看更多试卷

1

题型：填空题

|

填空题 · 5 分

已知某几何体的三视图如图所示，则该几何体的体积为

正确答案

12

解析

略

知识点

简单空间图形的三视图棱柱、棱锥、棱台的体积

1

题型：单选题

|

单选题 · 5 分

一个长方体被一平面截去一部分所得几何体的三视图如右图，

则该几何体的体积是：

A1 440

B1 200

C960

D720

正确答案

B

解析

略

知识点

组合几何体的面积、体积问题简单空间图形的三视图棱柱、棱锥、棱台的体积

1

题型：简答题

|

简答题 · 14 分

如图，内接于圆,是圆的直径，四边形

为平行四边形，平面 ,,

。

(1)求证：平面；

(2)设，表示三棱锥的体积，求函数的解析式及最大值，

正确答案

见解析。

解析

知识点

棱柱、棱锥、棱台的体积直线与平面垂直的判定与性质

1

题型：简答题

|

简答题 · 12 分

如图，在四棱锥中，底面为正方形，平面，已知，为线段的中点。

（1）求证：平面；

（2）求四棱锥的体积。

正确答案

见解析。

解析

(1) 连结和交于，连结，…………………………………………1分

为正方形，为中点，为中点，

， ……………………………………………………………………………4分

平面，平面

平面，……………………………………………5分

(2) 作于

平面，平面，，

为正方形，，平面，

平面， ………………………………………………………………………7分

，，平面 ………………………………8分

平面，平面，，

，， …………………………………………10分

四棱锥的体积 …………………………………………12分

知识点

棱柱、棱锥、棱台的体积直线与平面平行的判定与性质

1

题型：简答题

|

简答题 · 12 分

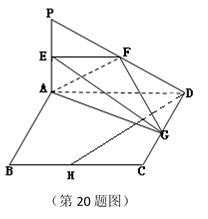
如图所示，PA⊥平面ABCD，四边形ABCD为正方形，且2PA=AD, E、F、G、H分别是线段PA、PD、CD、BC的中点.

（1）求证：BC∥平面EFG；

（2）求证：DH⊥平面AEG；

（3）求三棱锥E-AFG与四棱锥P-ABCD的体积比.

正确答案

见解析。

解析

（1）∵BC∥AD,AD∥EF,∴BC∥EF，，，，，，，，，。2分

∥平面EFG，，，，，，，，，，，。3分

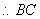
（2）∵PA⊥平面ABCD，∴PA⊥DH ，即 AE⊥DH，，，，，，，，，。5分

∵△ADG≌△DCH ，∴∠HDC=∠DAG，∠AGD+∠DAG=90°

∴∠AGD+∠HDC=90°

∴DH⊥AG

又∵AE∩AG=A，∴DH⊥平面AEG，，，，，，，，，，，。8分

（3），，，，，，，，，，，，，，。10分

，，，，，，，，，，，，，，。12分

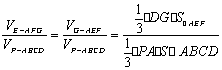
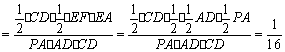
知识点

棱柱、棱锥、棱台的体积直线与平面平行的判定与性质直线与平面垂直的判定与性质

继续学习学习下一知识点

下一知识点 : 球的体积和表面积

百度题库 > 高考 > 文科数学 > 棱柱、棱锥、棱台的体积

扫码查看完整答案与解析