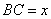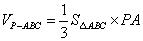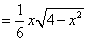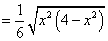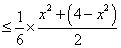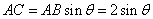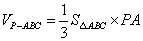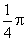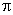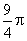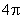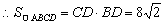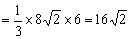- 棱柱、棱锥、棱台的体积
- 共170题
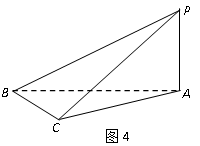
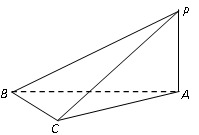
如图4, 在三棱锥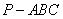
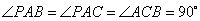
(1)求证:平面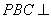
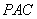
(2)若
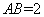
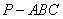
求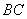
正确答案
见解析。
解析
(1)证明:因为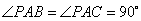

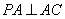
因为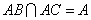
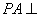
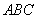
因为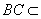
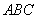
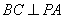
因为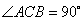
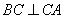
因为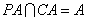
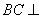
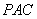
因为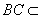
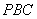
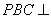
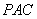
(2)
方法1:由已知及(1)所证可知,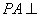
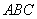
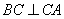
所以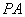

因为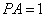
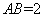
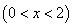
所以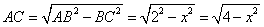
因为
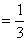
当且仅当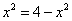
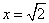
所以当三棱锥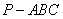
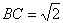
方法2:由已知及(1)所证可知,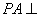
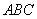
所以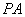

因为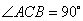
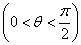
则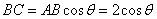
所以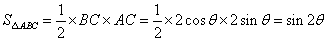
所以
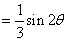
因为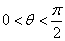
所以当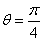
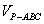
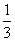
此时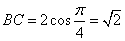
所以当三棱锥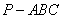
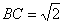
知识点
已知某几何体的三视图如右图所示,则该几何体的体积为
正确答案
解析
略
知识点
某几何体的三视图如图所示,则它的体积为______.
正确答案
16
解析
略
知识点
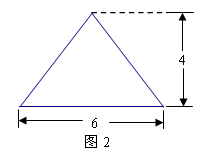
一个圆锥的正(主)视图及其尺寸如图2所示,若一个平行于
圆锥底面的平面将此圆锥截成体积之比为1﹕7的上、下两
部分,则截面的面积为
正确答案
解析
略
知识点
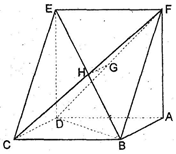
已知如图:平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点。
(1)求证:GH∥平面CDE;
(2)若CD=2,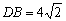
正确答案
见解析。
解析
(1)证法:∵EF//AD, AD//BC ∴EF//BC且EF=AD=BC
∴四边形EFBC是平行四边形 ∴H为FC的中点
又∵G是FD的中点
∴HG//CD
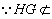
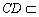
∴GH//平面CDE
证法2:连结EA,∵ADEF是正方形 ∴G是AE的中点
∴在△EAB中,GH//AB
又∵AB//CD,∴GH//CD,
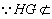
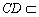
∴GH//平面CDE
(2)∵平面ADEF⊥平面ABCD,交线为AD
且FA⊥AD, ∴FA⊥平面ABCD,
∵BC=6, ∴FA=6 又∵CD=2,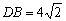
∴BD⊥CD
知识点
扫码查看完整答案与解析