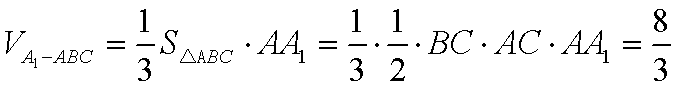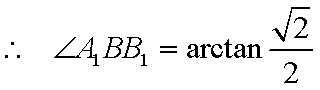- 棱柱、棱锥、棱台的体积
- 共170题
如图,多面体ABCDEFG中,四边形ABCD,CDEF都是边长为2的正方形,DE⊥平面ABCD,AG⊥平面ABCD,且AG=1。
(1)若P是BC的中点,证明AP∥平面BFG;
(2)求四面体ABEG的体积。
正确答案
见解析。
解析
(1)取BF中点Q,连PQ、GQ,则PQ∥CF,且PQ=
∵CDEF是正方形,DE⊥平面ABCD,
∴ CF⊥平面ABCD,
∴PQ⊥平面ABCD,
又AG⊥平面ABCD,
∴PQ∥AG,APQG为矩形,
∴AP∥GQ
∵QG

∴AP∥平面BFG
(2)∵AG⊥平面ABCD,∴AG⊥AD,
又ABCD是矩形,∴AB⊥AD
从而AD⊥平面ABG
又DE⊥平面ABCD,∴AG∥DE
∴
知识点
如图,菱形







(1)求证:
(2)求三棱锥
正确答案
见解析
解析
解析:(1) 证明:由题意,
因为


又因为菱形

因为


因为



(2)解:三棱锥

由(1)知,

所以



所求体积等于
知识点
如图所示,圆柱的高为2,底面半径为


(1)求证
(2)求四棱锥E-ABCD的体积。
正确答案
见解析。
解析
(1)证明:



又







(2)因为母线


由(1)知






过



又







设正方形


又

在



知识点
如图,在直三棱柱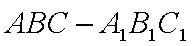
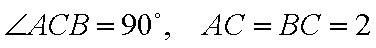
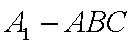
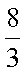
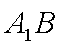
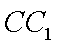

正确答案
见解析
解析
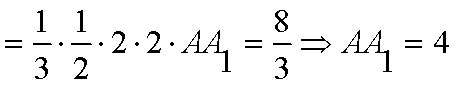
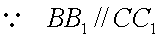
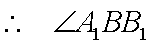
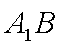
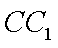
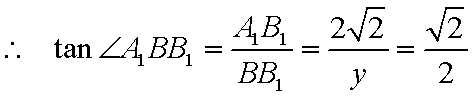
所以直线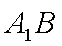
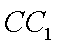
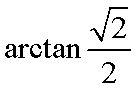
知识点
19.如图,已知四棱锥







(1)求证:
(2)求 四棱锥
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析