- 利用基本不等式求最值
- 共109题
设第一象限内的点(



正确答案
解析
作出可行域如图,由















知识点
设第一象限内的点(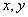
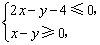
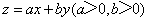
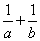
正确答案
解析
作出可行域如图,由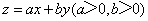
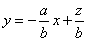
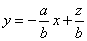
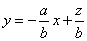
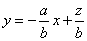
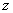
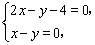
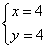
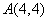
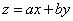
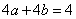
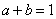
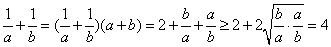
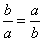
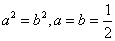
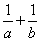
知识点
实数


正确答案
解析
略
知识点
对任意的a、b、c∈R+,代数式
正确答案
解析
任意的a,b、c∈R+,有

当且仅当


知识点
小张于年初支出50万元购买一辆大货车,第一年因缴纳各种费用需支出6万元,从第二年起,每年都比上一年增加支出2万元,假定该车每年的运输收入均为25万元,小张在该车运输累计收入超过总支出后,考虑将大货车作为二手车出售,若该车在第x年年底出售,其销售收入为25﹣x万元(国家规定大货车的报废年限为10年)。
(1)大货车运输到第几年年底,该车运输累计收入超过总支出?
(2)在第几年年底将大货车出售,能使小张获得的年平均利润最大?(利润=累计收入+销售收入﹣总支出)
正确答案
见解析。
解析
(1)设大货车运输到第x年年底,该车运输累计收入与总支出的差为y万元,
则y=25x﹣[6x+x(x﹣1)]﹣50=﹣x2+20x﹣50(0<x≤10,x∈N)
由﹣x2+20x﹣50>0,可得10﹣5
∵2<10﹣5
(2)∵利润=累计收入+销售收入﹣总支出,
∴二手车出售后,小张的年平均利润为

当且仅当x=5时,等号成立
∴小张应当再第5年将大货车出售,能使小张获得的年平均利润最大。
知识点
扫码查看完整答案与解析