· 基本不等式及不等式的应用

· 利用基本不等式求最值

利用基本不等式求最值
共109题

· 基本不等式及不等式的应用

· 利用基本不等式求最值

利用基本不等式求最值
共109题

热门试卷

X 查看更多试卷

1

题型：填空题

|

填空题 · 5 分

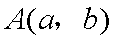
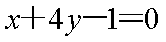
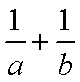
已知第一象限内的点在直线上，则的最小值为________。

正确答案

9

解析

略

知识点

利用基本不等式求最值

1

题型：填空题

|

填空题 · 5 分

设二次函数(为常数)的导函数为，对任意，不等式恒成立，则的最大值为________。

正确答案

解析

略

知识点

二次函数的图象和性质导数的运算利用导数研究函数的单调性利用基本不等式求最值

1

题型：填空题

|

填空题 · 5 分

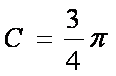
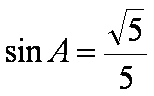
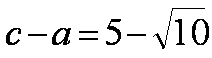
在△ABC中，角A，B，C，所对的边分别为a，b，c，且，，若，则b=________。

正确答案

解析

略

知识点

利用基本不等式求最值

1

题型：简答题

|

简答题 · 12 分

等差数列的各项均为正数，其前项和为，满足，且.

（1）求数列的通项公式；

（2）设，求数列的最小值项。

正确答案

（1）an=n（2）

解析

（1）由，可得.

又，可得. 数列是首项为1，公差为1的等差数列，. (4分)

（2）根据（1）得，.

由于函数在上单调递减，在上单调递增，

而，且，，

所以当时，取得最小值，且最小值为.

即数列的最小值项是. (12分)

知识点

由数列的前几项求通项等差数列的基本运算等差数列的前n项和及其最值利用基本不等式求最值

1

题型：单选题

|

单选题 · 5 分

设实数x和y满足约束条件，则z=2x+3y的最小值为（　　）

A26

B24

C16

D14

正确答案

D

解析

先根据约束条件画出可行域，

设z=2x+3y，

将最大值转化为y轴上的截距，

当直线z=2x+3y经过点A（4，2）时，z最大，

最大值是：2×4+3×2=14。

故选D。

知识点

利用基本不等式求最值

继续学习学习下一知识点

下一知识点 : 不等式与函数的综合问题

百度题库 > 高考 > 文科数学 > 利用基本不等式求最值

扫码查看完整答案与解析