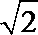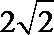- 利用基本不等式求最值
- 共109题
1
题型:
单选题
|
6.已知

正确答案
B
解析
解析已在路上飞奔,马上就到!
知识点
利用基本不等式求最值
1
题型:简答题
|
19.因发生意外交通事故,一辆货车上的某种液体泄露到一鱼塘中。为治理污染,根据环保部门的建议,现决定在鱼塘中投放一种可与污染液体发生化学反应的药剂。已知每投放



(1)若一次投放4个单位的药剂,则有效治污的时间可达几天?
(2)若因材料紧张,第一次只能投放2个单位的药剂,6天后再投放


正确答案
解:(1)因为 

①当



②当



综合得,
(2) 当


由题意知,

因为


故当且仅当


令



又

解析
解析已在路上飞奔,马上就到!
知识点
分段函数模型函数模型的选择与应用利用基本不等式求最值
1
题型:
单选题
|
4.设点

正确答案
A
解析
解析已在路上飞奔,马上就到!
知识点
利用基本不等式求最值两点间的距离公式
1
题型:
单选题
|
9. 有下列四个命题:
①对于



②所有指数函数的图象都经过点
③若实数


④已知两个非零向量



其中真命题的个数( )
正确答案
D
解析
解析已在路上飞奔,马上就到!
知识点
命题的真假判断与应用函数的周期性指数函数的单调性与特殊点数量积判断两个平面向量的垂直关系利用基本不等式求最值
1
题型:
单选题
|
4.正数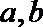
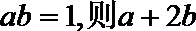
正确答案
B
解析
解析已在路上飞奔,马上就到!
知识点
利用基本不等式求最值
下一知识点 : 不等式与函数的综合问题
扫码查看完整答案与解析