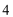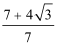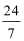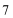- 利用基本不等式求最值
- 共109题
1
题型:简答题
|
18.某建筑公司用8000万元购得一块空地,计划在该地块上建造一栋至少12层.每层4000平方米的楼房。经初步估计得知,如果将楼房建为x(x
(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用=
正确答案
解:设楼房每平方米的平均综合费为

法一:
当且仅当
因此,当

为了使楼房每平方米的平均综合费最少,该楼房应建为20层,每平方米的平均综合费最小值为5000元
法二:
解析
解析已在路上飞奔,马上就到!
知识点
函数模型的选择与应用利用基本不等式求最值
1
题型:
单选题
|
9.设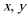
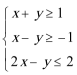
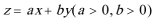
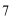
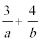
正确答案
D
解析
解析已在路上飞奔,马上就到!
知识点
求线性目标函数的最值利用基本不等式求最值
1
题型:
单选题
|
11.已知函数



正确答案
D
解析
解析已在路上飞奔,马上就到!
知识点
指数函数与对数函数的关系反函数利用基本不等式求最值
1
题型:填空题
|
7.设x,y均为正数,且
正确答案
49
解析


知识点
利用基本不等式求最值
1
题型:
单选题
|
6.在四边形ABCD中,M为AC上一点,且




正确答案
B
解析
解析已在路上飞奔,马上就到!
知识点
平面向量的基本定理及其意义利用基本不等式求最值
下一知识点 : 不等式与函数的综合问题
扫码查看完整答案与解析