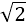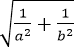- 利用基本不等式求最值
- 共109题
1
题型:填空题
|
15.已知总体的各值由小到大依次为2,3,3,7,a,b,12,13.7,18.3,20,且总体的中位数为10.5。若要使该总体的方差最小,则a,b的取值分别是________
正确答案
10.5 10.5
解析
这10个数的中位数为
要使总体方差最小,即要(a-10)2+(b-10)2最小,即a2+b2-20(a+b)+200最小,
∵a>0,b>0,∴a2+b2≥
又a+b=21,∴当a=b=10.5时,方差取得最小值。
知识点
利用基本不等式求最值众数、中位数、平均数极差、方差与标准差
1
题型:
单选题
|
6.已知a=(x,1),b=(2,-x),那么
正确答案
D
解析



若x=0,则
若x>0,由于


则0<


若x<0,由于-

则




即-

知识点
平面向量数量积的含义与物理意义利用基本不等式求最值
1
题型:
单选题
|
4.若直线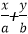
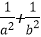
正确答案
B
解析
设向量m=(cosα,sinα),n=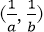
由题意知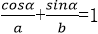
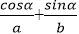
即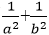
知识点
函数的最值利用基本不等式求最值
1
题型:
单选题
|
6.已知0<x<2,则
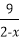
正确答案
C
解析
因为0<x<2,所以0<2-x<2,
所以
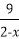

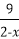
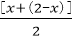
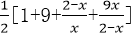
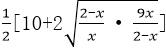
当且仅当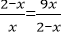

知识点
利用基本不等式求最值
1
题型:
单选题
|
4.若数列满足

正确答案
B
解析
依题意可得bn+1=pbn,则数列为等比数列。又b1b2b3…b99=599,所以b50=5,故b10·b90=
知识点
等比数列的判断与证明等比数列的性质及应用利用基本不等式求最值
下一知识点 : 不等式与函数的综合问题
扫码查看完整答案与解析