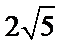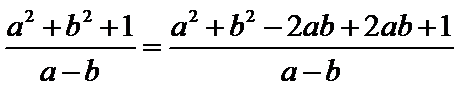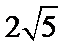- 利用基本不等式求最值
- 共109题
1
题型:填空题
|
13.若2x+2y=1,则x+y的取值范围是 。
正确答案
(-∞,-2],
解析


考查方向
本题主要考查了利用基本不等式来求解取值范围。
解题思路
本题考查采用基本不等式即可解出来。
易错点
本题考察了基本不等式,注意不等式的使用条件是一正二定三相等。
知识点
利用基本不等式求最值
1
题型:
单选题
|
8.已知a+b(a>0,b>0)是函数

正确答案
D
解析
1、由题可知,易得a+b=30-3a,即4a+b=30。
考查方向
本题主要考查了函数的零点及基本不等式,在近几年的各省高考题出现的频率较高。A选项不正确,B选项不正确,C选项不正确,所以选D选项。
解题思路
本题考查函数的零点及基本不等式,解题步骤如下:利用基本不等式求解即可
易错点
本题易在应用基本不等式的公式时发生错误。
知识点
函数零点的判断和求解利用基本不等式求最值
1
题型:填空题
|
13. 已知实数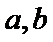
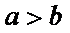
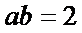
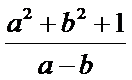
正确答案
解析
因为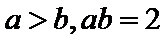
所以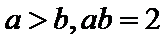
因为
所以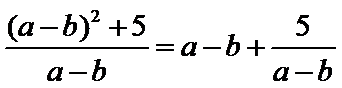
因为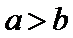
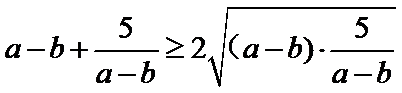
所以最小值为
考查方向
基本不等式
解题思路
先化简成基本不等式情况,然后再利用不等式性质求
易错点
想不到利用基本不等式,而是利用二次函数求最值
知识点
利用基本不等式求最值
1
题型:填空题
|
13.若2x+2y=1,则x+y的取值范围是 。
正确答案
(-∞,-2],
解析


考查方向
本题主要考查了利用基本不等式来求解取值范围。
解题思路
本题考查采用基本不等式即可解出来。
易错点
本题考察了基本不等式,注意不等式的使用条件是一正二定三相等。
知识点
利用基本不等式求最值
1
题型:
单选题
|
4.已知直线


正确答案
B
解析
连续抛掷两颗骰子得到的基本事件总数是





考查方向
本题主要考察了利用基本不等式求最值,考察了指数幂运算,该题属于简单题,
易错点
计算过程注意使用均值定理的条件
知识点
利用基本不等式求最值
下一知识点 : 不等式与函数的综合问题
扫码查看完整答案与解析