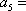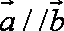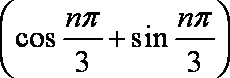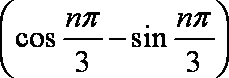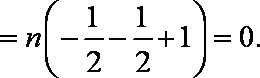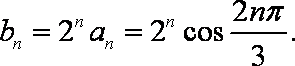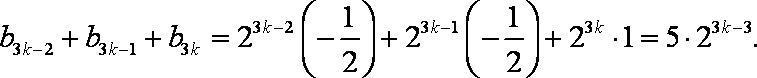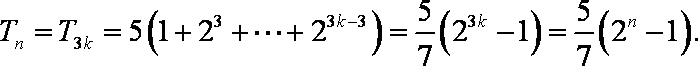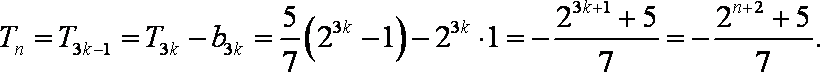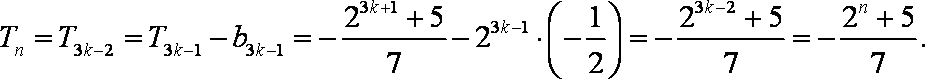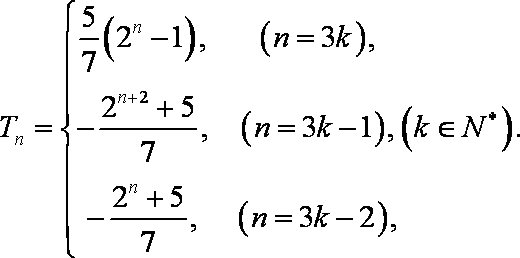- 等差数列
- 共618题
已知数列{an}满足




(1)求p的值及数列{an}的通项公式;
(2)设数列{bn}满足

正确答案
见解析
解析
(1)因为

所以

因为


所




所以 
依题意,
所以当n≥2时,

……


相加得
所以 
所以 
当n=1时,
所以 
(2)证明:因为 
所以 
因为 

若 



又因为 

所以
知识点
正数列




(1)求证:
(2)若数列
(3)若数列

正确答案
见解析
解析
(1)



(2)计算
根据数列是隔项成等差,写出数列的前几项:




当
所以




所以当

当
(3)因为数列
化简

设







只有
此时
或者
等差数列的前几项:



因为数列


此时
如果没有理由,猜想:


知识点
已知数列{an}中,a2=1,前n项和为Sn,且
(1)求a1,a3;
(2)求证:数列{an}为等差数列,并写出其通项公式;
(3)设
正确答案
见解析
解析
解析:(1)令n=1,则a1=S1=
(2)由


②-①,得 
于是,
③+④,得

又a1=0,a2=1,a2-a1=1,
所以,数列{an}是以0为首项,1为公差的等差数列。
所以,an=n-1。 9分
法二②-①,得 
于是,

(3)假设存在正整数数组(p,q),使b1,bp,bq成等比数列,
则lgb1,lgbp,lgbq成等差数列, 10分
于是,
所以,
当p≥3,且p∈N*时,
故数列{
于是

综上,存在唯一正整数数对(p,q)=(2,3),使b1,bp,bq成等比数列。
知识点
已知数列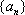

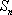
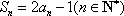
正确答案
解析
略
知识点
对大于或等于






根据上述分解规律,则


正确答案
9
解析
略
知识点
如下列所示,由若干个点组成形如三角形的图形,每条边(包括两个端点)有


正确答案

解析
略
知识点
对于任意的







(1)








(2)若各项为正数的等比数列







(3)若数列









正确答案
见解析
解析
解析:(1)在数列




在数列












(2)因为数列

将


解得

所以


对于任意的


所以数列数列


(3)由于

由于任意



即

即






即


只需

由① ②得

经检验

知识点
在数列






①若数列


②若数列



③等比数列一定是比等差数列,等差数列一定不是比等差数列;
④



其中所有真命题的序号是() .
正确答案
①②
解析
略
知识点
已知数列{an}满足:

(1)求证:数列
(2)求数列{an}的通项公式;
(3)求下表中前n行所有数的和Sn。
正确答案
见解析。
解析
知识点
记数列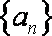
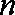
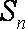
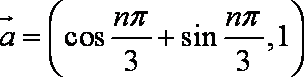
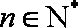
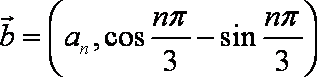
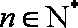
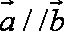
(1)求数列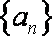
(2)求
(3)设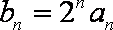
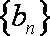
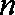
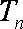
正确答案
见解析
解析
(1)∵
∴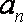
=
=
∴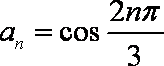
(2)数列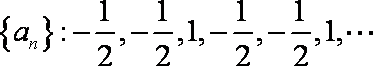
(3)
当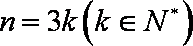
∵
∴
当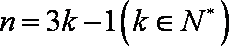
当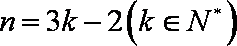
故
知识点
扫码查看完整答案与解析