- 等差数列
- 共618题
1.等差数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.在△ABC中,tanA是以

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知等差数列{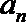
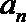
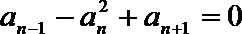
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
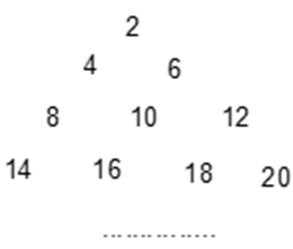
16.将正偶数排列如下表,其中第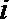
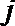
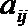
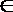
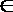
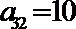
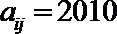
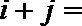
正确答案
60
解析
解析已在路上飞奔,马上就到!
知识点
20.已知


(1)若

(2)求证:对任意

正确答案
(1)依题意





所以
解得
(2)
设
则
考虑到
所以
又当

从而

所以对任意

解析
解析已在路上飞奔,马上就到!
知识点
8.已知等差数列





正确答案
解析
等价于
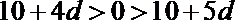

知识点
18.在数列


(1)证明数列

(2)设数列



正确答案
解:(1)


∴数列
∴
从而
(2)因为
所以
由


解析
解析已在路上飞奔,马上就到!
知识点
8.在



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若一组数据

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知{
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析