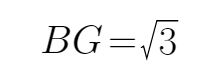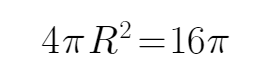- 球的体积和表面积
- 共46题
9.已知A,B是球O的球面上两点,∠AOB=90,C为该球面上的动点,若三棱锥O-ABC体
积的最大值为36,则球O的表面积为( )
正确答案
知识点
15.已知三棱锥




正确答案
12
解析
由已知得当PA,PB,PC两两互相垂直时三棱锥
O’为正



考查方向
解题思路
由已知得当PA,PB,PC两两互相垂直时三棱锥
易错点
1、三个侧面面积之和最大不能转化;2,给定一个正三棱锥不知如何寻找内接球半径。
知识点
11.如图ABCD -A1B1C1D1是边长为1的正方体,S- ABCD是高为l的正四棱锥,若点S,A1,B1,Cl,D1在同一个球面上,则该球的表面积为( )
正确答案
解析
按如图所示作辅助线,









故A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
解题思路
根据题意作图,找出球心位置,并设
故A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
球心的位置确定
知识点
10.点










正确答案
解析
由题意可知,0-ABC 为正三棱锥,设E点为三角形ABC的中心, 在正三角形ABC中,易求AE=1;在三角形OAE中,OE=1,又因为S到平面ABC的距离为1/2,所以S点所在的球小圆面与ABC所在的球小圆面之间的距离为1/2.所以OSE为等腰三角形,ES=S0=
考查方向
解题思路
画出草图,易得0-ABC 为正三棱锥,再求出OE=1,论证S的位置,最后得出OSE为等腰三角形,求得SE=
易错点
本题对空间要求的能力较高,易在理解题中的位置关系与数量关系及作图中出错
知识点
14.四面体ABCD的四个顶点都在球O的表面上,AB⊥平面BCD,三角形BCD是边长为3的等边三角形,若AB=2,则球O的表面积为_________.
正确答案
解析
取CD的中点E,连接AE,BE,因为四面体ABCD中,AB垂直平面BCD,三角形BCD是边长为3的等边三角形。
所以三角形ABC和三角形ABD全等,三角形ACD是等腰三角形
可求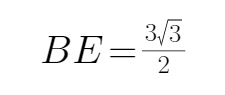
所以R=2,所以四面体ABCD外接球的表面积为:
考查方向
球的体积和表面积
解题思路
取CD的中点E,连接AE,BE,作出外接球的球心,求出半径,即可求出表面积。
易错点
不能作出正确的辅助线
知识点
正确答案
知识点
正确答案
知识点
10.已知三棱锥




正确答案
解析
在三角形ABC中,
所以三角形ABC的外接圆半径
三棱锥外接球的半径
所以三棱锥P-ABC外接球的表面积
考查方向
球的体积的计算,棱锥的外接球
解题思路
根据已知求出△ABC外接圆的半径,从而求出该三棱锥外接球的半径和三棱锥的外接球表面积
易错点
空间立体感弱,找不到、求不出三棱锥的外接球半径
教师点评
本题考察三棱锥的外接球的表面积的求法,关键在于找到外接球的半径并求出它。
知识点
9.已知A,B是球O的球面上两点,∠AOB=90,C为该球面上的动点,若三棱锥O-ABC体积的最大值为36,则球O的表面积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析