绝对值不等式
共8题

· 绝对值不等式

绝对值不等式
共8题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 15 分

已知函数，.

24.若，且关于的不等式在上有解，求的最小值；

25.若函数在区间上不单调，求的取值范围．

第(1)小题正确答案及相关解析

正确答案

；

解析

试题分析：本题属于分段函数的性质、函数的最值、函数的单调性的综合应用问题，属于拔高题，不易得分，解析如下：当时，

结合图象可知，

函数在上单调递减，在上单调递增，

，由已知得，有解，只要，所以，

即的最小值为.

考查方向

本题考查了分段函数的性质、函数的最值、函数的单调性等知识点。

解题思路

先求出函数的最值，再利用恒成立求实数的最小值；

易错点

第二问中忽略对实数a范围的讨论导致出错。

第(2)小题正确答案及相关解析

正确答案

或．

解析

试题分析：本题属于分段函数的性质、函数的最值、函数的单调性的综合应用问题，属于拔高题，不易得分，解析如下：

（1）若，则在上单调递增，不满足条件；

（2）若，则，所以,

在上递减，在上递增，

故在上不单调等价于：解得；

（3）若，则

结合图象，有以下三种情况：

当，即时，函数在上单调递增，在上单调递减，在上不单调等价于解得；

当，即时，函数在上单调递减，在上单调递增，由于恒成立，

所以在区间上不单调成立，即符合题意；

③当时，在上递减，在上递增，因此在上不单调，符合题意. 综上所述，或.

考查方向

本题考查了分段函数的性质、函数的最值、函数的单调性等知识点。

解题思路

根据题中条件就参数a的范围进行分类讨论，结合函数在区间上不单调，即可求除的取值范围．

易错点

第二问中忽略对实数a范围的讨论导致出错。

题型：填空题

填空题 · 5 分

13．若，则关于的不等式的解集为___________

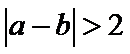
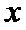
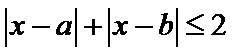
正确答案

解析

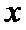
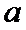
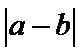
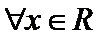
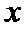
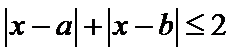
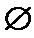
根据绝对值的意义，表示数轴上的对应点到和的对应点的距离之和，故最小值为，所以对满足故关于的不等式的解集为.

考查方向

本题主要考查绝对值不等式的几何意义，绝对值三角不等式等知识，意在考查考生的数形结合能力和转化与化归的能力。

解题思路

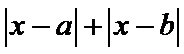
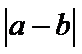
1.先根据绝对值的几何意义得到的最小值为，2.所以所求不等式的解集即可得到。

易错点

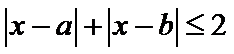
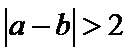
1.不会将题中要求的结构与题中给出的结构之间建立联系；2.对于解集为空集存在怀疑。

知识点

绝对值不等式

题型：单选题

单选题 · 5 分

9.若x、y满足，则的取值范围是（）

正确答案

解析

表示的平面区域为直线所围成的正方形区域，变形为，当其经过点（1,0）时，z最大为2，当其经过点（-1,0）时，z最小为-2，故z的取值范围为，选B。

考查方向

本题主要考查线性规划的有关知识，意在考查考生数形结合、分类讨论的数学思想。

解题思路

1.先做出约束条件对应的可行域；2.求出可行域端点的坐标，将各个点带入目标函数z的最大值和最小值即可。

易错点

对应的可行域是什么不会画；

知识点

绝对值不等式不等式的基本性质

题型：填空题

填空题 · 5 分

15．（请在A.B两题中任选一题做）

A．（坐标系与参数方程选做题）

已知极坐标的极点在直角坐标系的原点O处，极轴与x轴的正半轴重合，曲线C的参数方程为（为参数），直线l的极坐标方程为．点P在曲线C上，则点P到直线l的距离的最小值为_______.

B．（不等式选讲选做题）

关于x的不等式的解集为空集，则实数a的取值范围是________.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

绝对值不等式

题型：单选题

单选题 · 5 分

1．设，若，则下列不等式中正确的是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

绝对值不等式比较法

继续学习学习下一知识点

下一知识点 : 不等式的基本性质

百度题库 > 高考 > 理科数学 > 绝对值不等式

扫码查看完整答案与解析