- 平面向量的概念辨析
- 共54题
已知






(1)求
(2)若存在一条与




(3)当实数

正确答案
见解析。
解析
(1)



关于


也就是不等式

∴


由韦达定理得:
∴
(2)由(1)得








令
当



从而

(3)

∴
方程

①若

或
则



∴函数


此时函数


②若






此时

下面只需考虑
由


当
故

∴函数

∴函数
当
则





∴函数



此时函数


综上所述, 若



若






知识点
随机变量ξ服从正态分布N(40, 
正确答案
0.6
解析

所以
知识点
若



正确答案
解析
因为







知识点
已知向量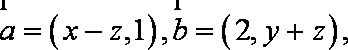

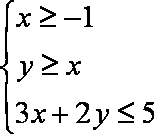
正确答案
解析
由

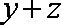
画出不等式组的可行域,如右图,目标函数变为: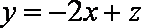
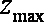
知识点
在△ABC中,∠A=90°,AB=1,AC=2,设点P,Q满足

正确答案
解析
由题意可得

由于




=0﹣(1﹣λ)

解得 λ=
故答案为:
知识点
扫码查看完整答案与解析