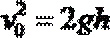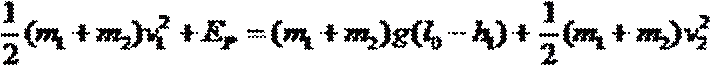- 动量守恒定律
- 共299题
19.如图所示,水平传送带AB距离地面的高度为h,以恒定速率v0顺时针运行。甲、乙两相同滑块(视为质点)之间夹着一个压缩轻弹簧(长度不计),在AB的正中间位置轻放它们时,弹簧立即弹开,两滑块以相同的速率分别向左、右运动。下列判断正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
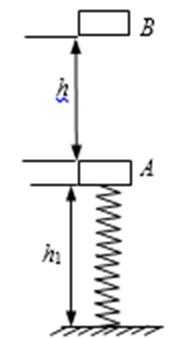
21.如图所示,一轻质弹簧竖直固定在地面上,自然长度l0=0.50m,上面连接一个质量m1=1.0kg的物体A,平衡时物体距地面h1=0.40m,此时弹簧的弹性势能EP=0.50J。在距物体A正上方高为h=0.45m处有一个质量m2=1.0kg的物体B自由下落后,与弹簧上面的物体A碰撞并立即以相同的速度运动,已知两物体不粘连,且可视为质点。g=10m/s2。
求:
(1)碰撞结束瞬间两物体的速度大小;
(2)两物体一起运动第一次具有竖直向上最大速度时弹簧的长度;
(3)两物体第一次分离时物体B的速度大小。
正确答案
(1)设物体B自由下落与物体A相碰时的速度为v0,则
解得:v0=3.0m/s
设A与B碰撞结束瞬间的速度为v1,根据动量守恒定律
m2 v0=(m1+ m2)v1,
解得:v1=1.5 m/s,
(2)设物体A静止在弹簧上端时弹簧的压缩量为x1,
x1=l0-h1=0.10m
设弹簧劲度系数为k,根据胡克定律有m1g=kx1
解得:k=100N/m
两物体向上运动过程中,弹簧弹力等于两物体总重力时具有最大速度,
设此时弹簧的压缩量为x2,则(m1+ m2)g=kx2,
解得:x2=0.20m,
设此时弹簧的长度为l,则l=l0-x2
解得:l=0.30m
(3)两物体向上运动过程中在弹簧达到原长时分离,
从碰后到分离的过程,物体和弹簧组成的系统机械能守恒,
解得:v2=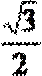
解析
解析已在路上飞奔,马上就到!
知识点
15.如图所示,水平面上停放着A,B两辆小车,质量分别为M和m, M>m,两小车相距为L,人的质量也为m,另有质量不计的硬杆和细绳。第一次人站在A车上,杆插在B车上;第二次人站在B车上,杆插在A车上;若两种情况下人用相同大小的水平作用力拉绳子,使两车相遇,不计阻力,两次小车从开始运动到相遇的时间分别为t1和t2,则( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.“轨道电子俘获”也是放射性同位素衰变的一种形式,它是指原子核(称为母核)俘获一个核外电子,其内部一个质子变为中子,从而变成一个新核(称为子核),并且放出一个中微子的过程。中微子的质量很小,不带电,很难被探测到,人们最早就是通过子核的反冲而间接证明中微子的存在。一个静止原子的原子核发生“轨道电子俘获”,衰变为子核并放出中微子。下面说法中正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
请考生从给出的3道物理题、3道化学题、2道生物题中每科任选一题做答。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析