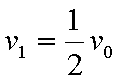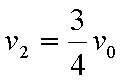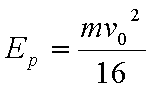- 动量守恒定律
- 共299题
如图,质量为M、长为L、高为h的矩形滑块置于水平地面上,滑块与地面间动摩擦因数为μ;滑块上表面光滑,其右端放置一个质量为m的小球。用水平外力击打滑块左端,使其在极短时间内获得向右的速度v0,经过一段时间后小球落地。求小球落地时距滑块左端的水平距离。
正确答案
见解析。
解析
在m从右边缘至左边缘时M的加速度
设此时M的速度为v1,所以可得
在m离开M做自由落体运动时,M的加速度
讨论
(1)当m落地使M已停止,那么

(2)当m落地使M未停止,那么


知识点
(1)氢原子能级如图,当氢原子从

a. 氢原子从

b. 用波长为325nm的光照射,可使氢原子从

c. 一群处于
d. 用波长为633nm的光照射,不能使氢原子从

(2)如图,光滑水平直轨道上两滑块A.B用橡皮筋连接,A的质量为m。开始时橡皮筋松驰,B静止,给A向左的初速度v0。一段时间后,B与A同向运动发生碰撞并粘在一起。碰撞后的共同速度是碰撞前瞬间A的速度的两倍,也是碰撞前瞬间B的速度的一半。求:
(ⅰ)B的质量;
(ⅱ)碰撞过程中A.B系统机械能的损失。
正确答案
(1)cd
(2)解:
(ⅰ)以初速度v0的方向为正方向,设B的质量为mB,A.B碰撞后的共同速度为v,由题意知:碰撞前瞬间A的速度为

由①式得 
(ⅱ)从开始到碰后的全过程,由动量守恒定律得

设碰撞过程A.B系统机械能的损失为

联立②③④式,得
解析
略。
知识点
如图所示,竖直平面内的四分之一圆弧轨道下端与水平桌面相切,小滑块A和B分别静止在圆弧轨道的最高点和最低点。现将A无初速度释放,A与B碰撞后结合为一个整体,并沿桌面滑动。已知圆弧轨道光滑,半径R=0.2m;A和B的质量相等;A和B整体与桌面之间的动摩擦因数
(1) 碰撞前瞬间A的速率v;
(2) 碰撞后瞬间A和B整体的速率
(3) A和B整体在桌面上滑动的距离
正确答案
答案:(1)

解析
(1)滑块从圆弧最高点滑到最低点的过程中,根据机械能守恒定律,有
(2)滑块A与B碰撞,根据动量守恒定律,有
(3)滑块A与B粘在一起滑行,根据动能定理,有
知识点
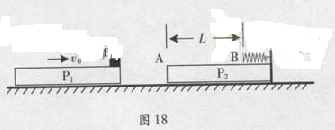
图18,两块相同平板P1、P2至于光滑水平面上,质量均为m。P2的右端固定一轻质弹簧,左端A与弹簧的自由端B相距L。物体P置于P1的最右端,质量为2m且可以看作质点。P1与P以共同速度v0向右运动,与静止的P2发生碰撞,碰撞时间极短,碰撞后P1与P2粘连在一起,P压缩弹簧后被弹回并停在A点(弹簧始终在弹性限度内)。
(1)P1、P2刚碰完时的共同速度v1和P的最终速度v2;
(2)此过程中弹簧最大压缩量x和相应的弹性势能Ep
正确答案
见解析
解析
(1)p1和p2碰撞动量守恒:
mv0=(m+m)v1 ①
得出:
P在p2上滑行过程 p1、p2、p系统动量守恒:
2mv0+2mv1=4mv2 ②
得出:
(2)p1 p2 p第一次等速弹簧最大压缩量最大,由能量守恒得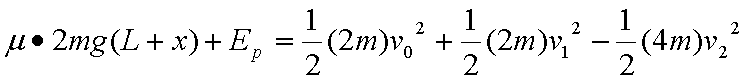
p刚进入p2 到p1 p2 p 第二次等速时有能量守恒得;
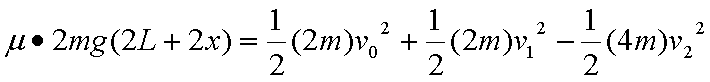
由③④得: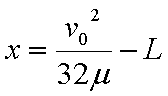
知识点
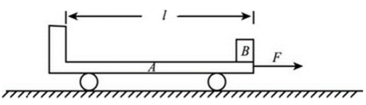
如图所示,水平地面上静止放置一辆小车A,质量mA=4kg,上表面光滑,小车与地面间的摩擦力极小,可以忽略不计。可视为质点的物块B置于A的最右端,B的质量mB=2kg.现对A施加一个水平向右的恒力F=10N,A运动一段时间后,小车左端固定的挡板与B发生碰撞,碰撞时间极短,碰后A、B粘合在一起,共同在F的作用下继续运动,碰撞后经时间t=0.6s,二者的速度达到vt=2m/s.求
(1)A开始运动时加速度a的大小;
(2)A、B碰撞后瞬间的共同速度v的大小;
(3)A的上表面长度l
正确答案
(1)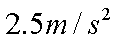
(2)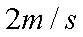
(3)0.45
解析
(1)以A为研究对象,由牛顿第二定律有
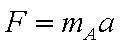
代入数据解得
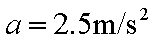
(2)对A,B碰撞后共同运动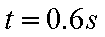
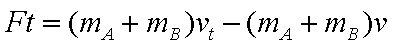
代入数据解得
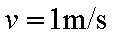
(3)设A,B发生碰撞前,A的速度为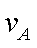
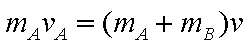
A从开始运动到与B发生碰撞前,由动能定理有
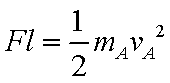
由④⑤⑥式,代入数据解得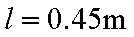
知识点
扫码查看完整答案与解析