- 椭圆的定义及标准方程
- 共448题
22.如图已知椭圆






(1)求椭圆
(2)已知垂直于








(3)在






正确答案
(1)由题设得
解得: 
故

(2)证明:

直线

①×②,得

代入③得

因为点


即点

(3)设直线
结合第(2)问的结论

所以
解析
解析已在路上飞奔,马上就到!
知识点
已知椭圆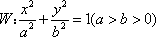

(1)求椭圆W的方程.
(2)设斜率为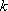
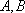
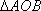
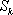
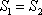
正确答案
见解析
解析
(1)解:由题意,得椭圆W的半焦距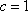
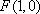
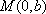
所以直线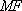
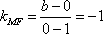
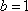
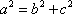
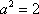
所以椭圆W的方程为
(2)证明:设直线l的方程为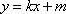
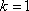
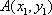
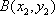
由方程组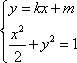
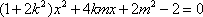
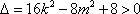
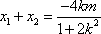
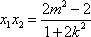
所以 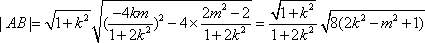
因为原点
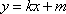
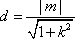
所以 
当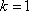
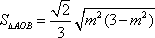
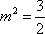
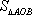
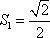
当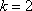
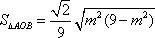


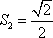
所以 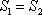
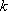
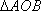
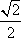
知识点
已知椭圆



正确答案
解析
知识点
已知中心在原点O,焦点F1、F2在x轴上的椭圆E经过点C(2,2),且抛物线
(1)求椭圆E的方程;
(2)垂直于OC的直线ι与椭圆E交于A、B两点,当以AB为直径的圆P与y轴相切时,求直线ι的方程和圆P的方程。
正确答案
见解析。
解析
(1)设椭圆E的方程为




由①、②、③得a2=12,b2=6
所以椭圆E的方程为
(2)依题意,直线OC斜率为1,由此设直线ι的方程为y=-x+m,
代入椭圆E方程,得

当m=3时,直线ι方程为y=-x+3,此时,x1 +x2=4,圆心为(2, 1),半径为2,
圆P的方程为(x-2)2+(y-1)2=4;
同理,当m=-3时,直线ι方程为y=-x-3,
圆P的方程为(x+2)2+(y+1)2=4;
知识点
已知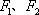
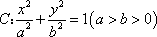
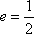
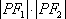
(1)求椭圆C的标准方程;
(2)过右焦点F2作斜率为k的直线l与椭圆C交于M、N两点,在x轴上是否存在点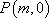
正确答案
见解析。
解析
知识点
扫码查看完整答案与解析