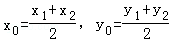- 椭圆的定义及标准方程
- 共448题
已知椭圆的中心在原点,焦点在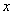
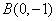
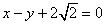
(1)求椭圆方程;
(2)设直线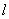
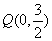

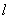
正确答案
见解析。
解析
(1)设椭圆方程为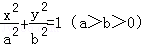
设右焦点F(c,0)(c>0),则由条件得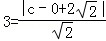
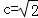
则a2=b2+c2=3,
∴椭圆方程为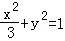
(2)若直线l斜率不存在时,直线l即为y轴,此时M,N为椭圆的上下顶点,|BN|=0,|BM|=2,不满足条件;
故可设直线l: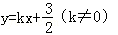
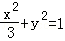
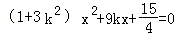
由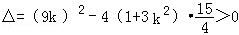
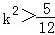
设M(x1,y1),N(x2,y2),MN的中点P(x0,y0),
由韦达定理得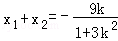
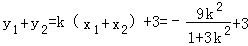
则
由|BN|=|BM|,则有BP⊥MN,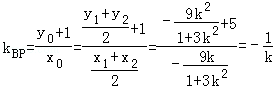
可求得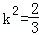
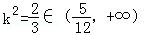
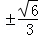
所以直线l的方程为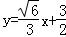
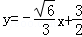
知识点
已知






(1)求圆
(2)设过点







正确答案
见解析。
解析
(1) 先求圆C关于直线x + y – 2 = 0对称的圆D,由题知圆D的直径为


(2)由(1)知


圆C:



由椭圆的焦半径公式得:

所以当
知识点
如图,已知椭圆










(1)求椭圆
(2)求

(3)设点








正确答案
见解析。
解析
(1)
故椭圆

(2)点






由于点


由已知




由于



由(*)式,





故圆

(3)
知识点
如图,椭圆




(1)求椭圆M的标准方程;
(2)设直线



正确答案
见解析。
解析
(1)
矩形ABCD面积为8,即
由①②解得:
∴椭圆M的标准方程是
(2)
设

由


当





①当


其中




②由对称性,可知若



③当


由此知,当


综上可知,当


知识点
设

(1)设椭圆C上的点


(2)设过(1)中所得椭圆上的焦点


(3)设点P是椭圆C 上的任意一点,过原点的直线



正确答案
见解析。
解析
(1)由于点
解得
故椭圆C的方程为
(2)由(1)知椭圆C的左右焦点坐标分别为
所以, 过椭圆的焦点
将其代入

当


所以
(3)过原点的直线L与椭圆




两式相减得
又∵
故:

知识点
扫码查看完整答案与解析