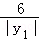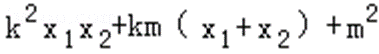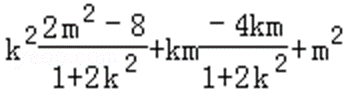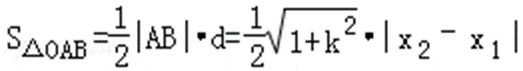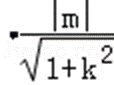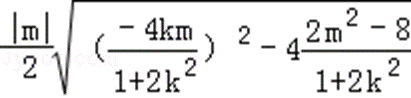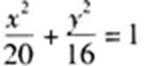- 椭圆的定义及标准方程
- 共448题
19.设椭圆
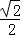

(Ⅰ)求a、b的值;
(Ⅱ)设M、N是右准线l上两动点,满足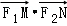
正确答案
(I)因为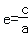
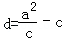
所以由题设得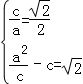
解得,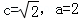
由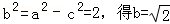
(Ⅱ)证明:由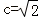
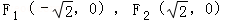
则l的方程为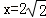
故可设
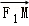
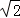
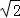
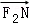

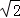
由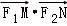
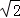
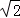
得y1y2=﹣6,所以y1y2≠0,
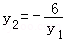
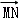


当且仅当
即M,N两点关于x轴对称.
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆
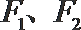
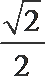

(I)求椭圆的方程;
(II)证明: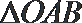
正确答案
(I)由椭圆的离心率为
可得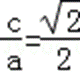

又2a=|AF1|+|AF2|=
∴a=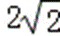
∴b2=4,
∴椭圆方程为: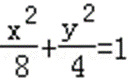
(Ⅱ)设直线AB的方程为y=kx+m,
再设A(x1,y1),B(x2,y2),
联立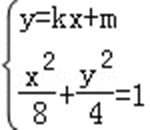
可得(1+2k2)x2+4kmx+2m2﹣8=0
△=(4km)2﹣4(1+2k2)(2m2﹣8)=8(8k2﹣m2+4)>0,

∵
∴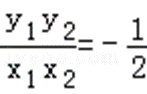
∴
又y1y2=(kx1+m)(kx2+m)
=
=
=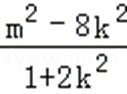
∴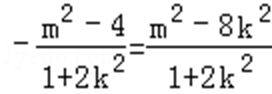
∴﹣(m2﹣4)=m2﹣8k2,即4k2+2=m2,
设原点到直线AB的距离为d,
则
=
=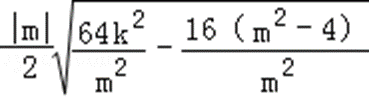
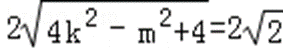
∴当直线斜率不存在时,有A(
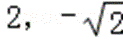
S△OAB=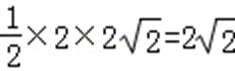
即△OAB的面积为定值2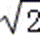
解析
解析已在路上飞奔,马上就到!
知识点
19.已知椭圆C:


(I)求椭圆C的方程;
(Ⅱ)设M是椭圆的上顶点,过点M分别作直线MA,MB交椭圆于A,B两点,设两直线的斜率分别为k1,k2,且k1+k2=4,证明:直线AB过定点N(
正确答案
(I)由已知得:
解得
故椭圆方程为:
(Ⅱ)由(I)知M(0,1),设MA:y=k1x+1,
由

则

所以A(﹣



所以



所以




故

解析
解析已在路上飞奔,马上就到!
知识点
14.若椭圆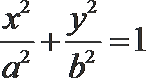
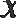
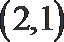
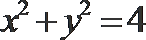
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知椭圆C:


(I)求椭圆C的方程;
(II)已知动直线
①若线段AB中点的横坐标为
②已知点M(

正确答案
(I)因为


解得
则椭圆方程为
(II)①将

因为AB中点的横坐标为-
所以
②由①知
所以
=
=
=
=
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析