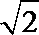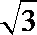- 椭圆的定义及标准方程
- 共448题
19. 设椭圆






(Ⅰ)若过


(Ⅱ)在(Ⅰ)的条件下,过右焦点









正确答案
(Ⅰ)由题意


又



所以
所以

又过




故所求椭圆方程为
(Ⅱ)由()知


椭圆联立方程得

设交点为

则
若存在点

由于菱形对角线垂直,所以

又




由已知条件知





解析
解析已在路上飞奔,马上就到!
知识点
22.如图已知,椭圆




(Ⅰ)若

(Ⅱ)若

正确答案
解:(I)




(II)

①若



②若AB与


则直线
由








∴
综合①、②可得:







解析
解析已在路上飞奔,马上就到!
知识点
22.已知椭圆C:



(Ⅰ)用m表示点E,F的坐标;
(Ⅱ)证明直线EF与y轴交点的位置与m无关.
正确答案
(Ⅰ)







直线BM的方程为y=
得
由
得

(Ⅱ)据已知,



令x=0,得

解析
解析已在路上飞奔,马上就到!
知识点
10.已知椭圆C: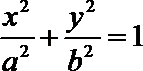

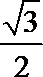
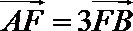
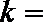
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知椭圆





(Ⅰ)求椭圆的方程;
(Ⅱ)若线段AB的中点的横坐标为

(Ⅲ)在


正确答案
(Ⅰ)∵椭圆离心率为

又



∴椭圆方程为

(Ⅱ) ∵直线L过点C(-1,0)且斜率为K,
则设直线方程为
由

若上式是与K无关的常数,则6m-1=0,∴
即在x轴上存在点M(

解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析