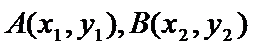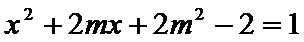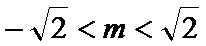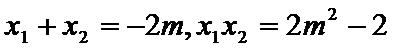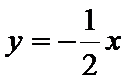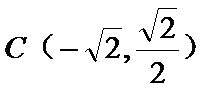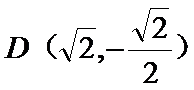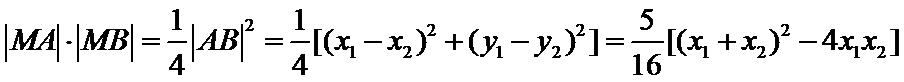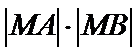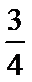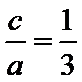椭圆的定义及标准方程_章节学习

1

题型：单选题

|

单选题 · 5 分

12.已知O为坐标原点，F是椭圆C：的左焦点，A，B分别为C的左，右顶点。P为C上一点，且PF⊥x轴。过点A的直线l与线段PF交于点M，与y轴交于点E。若直线BM经过OE的中点，则C的离心率为

A

B

C

D

正确答案

A

知识点

椭圆的定义及标准方程

1

题型：简答题

|

简答题 · 13 分

已知椭圆E：+=1(a﹥b﹥0)的一个焦点与短轴的两个端点是正三角形的三个顶点，点P(，)在椭圆E上。

25.求椭圆E的方程；

26.设不过原点O且斜率为的直线l与椭圆E交于不同的两点A，B，线段AB的中点为M，直线OM与椭圆E交于C，D，证明：︳MA︳·︳MB︳=︳MC︳·︳MD︳

第(1)小题正确答案及相关解析

正确答案

（1）；

解析

（I）由已知，a=2b.

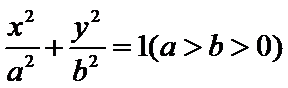
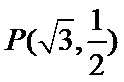
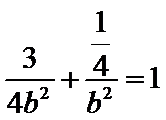
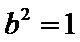
又椭圆过点，故，解得.

所以椭圆E的方程是.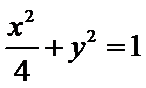

考查方向

本题考查椭圆的标准方程及其几何性质，考查学生的分析问题解决问题的能力和数形结合的思想.在涉及到直线与椭圆（圆锥曲线）的交点问题时，一般都设交点坐标为，同时把直线方程与椭圆方程联立，消元后，可得，再把用表示出来，并代入刚才的，这种方法是解析几何中的“设而不求”法．可减少计算量，简化解题过程

解题思路

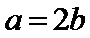
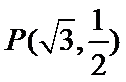
由椭圆两个焦点与短轴的一个端点是正三角形的三个顶点可得，椭圆的标准方程中可减少一个参数，再利用在椭圆上，可解出b的值，从而得到椭圆的标准方程；

易错点

本题考查椭圆的标准方程及其几何性质，考查学生的分析问题解决问题的能力和数形结合的思想.在涉及到直线与椭圆（圆锥曲线）的交点问题，联立化简易出错。

第(2)小题正确答案及相关解析

正确答案

(Ⅱ)设直线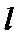的方程为，

由方程组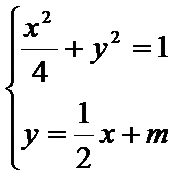得

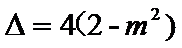
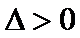
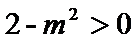
判别式为，由，即，解得

由根与系数的关系可得

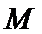
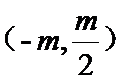
所以点的坐标为，直线的方程为

联立可得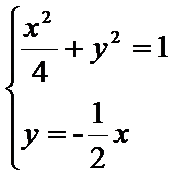得

所以.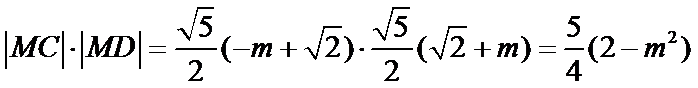

又

.

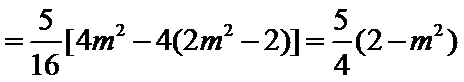
所以.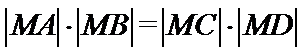

解析

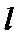
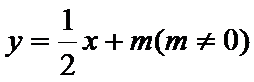
(Ⅱ)设直线的方程为，

由方程组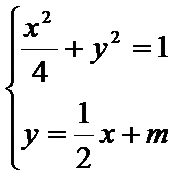得

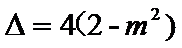
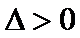
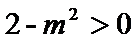
判别式为，由，即，解得

由根与系数的关系可得

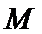
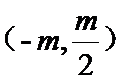
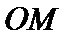
所以点的坐标为，直线的方程为

联立可得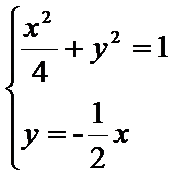得

所以.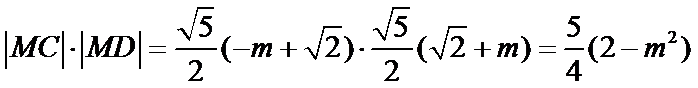

又

.

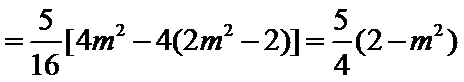
所以.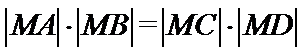

考查方向

本题考查椭圆的标准方程及其几何性质，考查学生的分析问题解决问题的能力和数形结合的思想.在涉及到直线与椭圆（圆锥曲线）的交点问题时，一般都设交点坐标为，同时把直线方程与椭圆方程联立，消元后，可得，再把用表示出来，并代入刚才的，这种方法是解析几何中的“设而不求”法．可减少计算量，简化解题过程

解题思路

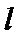
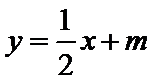
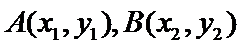
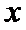
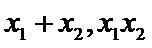
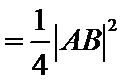
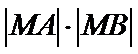
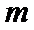
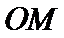
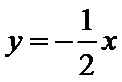
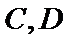
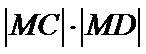
（Ⅱ）首先设出直线方程为，同时设交点，把方程与椭圆方程联立后消去得的二次方程，利用根与系数关系，得，由求得（用表示），由方程具体地得出坐标，也可计算出，从而证得相等．

易错点

本题考查椭圆的标准方程及其几何性质，考查学生的分析问题解决问题的能力和数形结合的思想.在涉及到直线与椭圆（圆锥曲线）的交点问题，联立化简易出错。

1

题型：填空题

|

填空题 · 13 分

已知椭圆E：+=1(a﹥b﹥0)的一个焦点与短轴的两个端点是正三角形的三个顶点，点P(，)在椭圆E上。

(Ⅰ)求椭圆E的方程；

(Ⅱ)设不过原点O且斜率为的直线l与椭圆E交于不同的两点A，B，线段AB的中点为M，直线OM与椭圆E交于C，D，证明：︳MA︳·︳MB︳=︳MC︳·︳MD︳

正确答案

（I）由已知，a=2b.

又椭圆过点，故，解得.

所以椭圆E的方程是.

（II）设直线l的方程为，，

由方程组得，①

方程①的判别式为，由，即，解得.

由①得.

所以M点坐标为，直线OM方程为，

由方程组得.

所以.

又

.

所以.

知识点

椭圆的定义及标准方程椭圆的几何性质

1

题型：填空题

|

填空题 · 5 分

10.如图，在平面直角坐标系xOy中，F是椭圆的右焦点，直线与椭圆交于B，C两点，且 ,则该椭圆的离心率是 .

正确答案

知识点

椭圆的定义及标准方程

1

题型：单选题

|

单选题 · 5 分

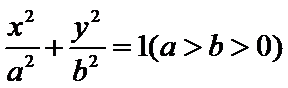
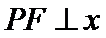
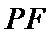
12.已知O为坐标原点，F是椭圆C：的左焦点，A，B分别为C的左，右顶点.P为C上一点，且轴.过点A的直线l与线段交于点M，与y轴交于点E.若直线BM经过OE的中点，则C的离心率为

A

B

C

D

正确答案

A

解析

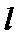
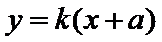
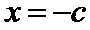
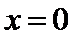
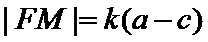
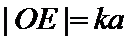
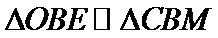
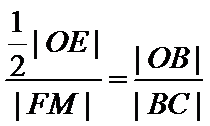
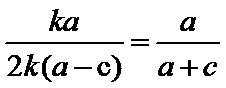
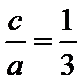
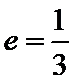
由题意设直线的方程为，分别令与得点，

，由，得，即，整理，得，所以椭圆离心率为，故选A．

考查方向

本题主要考查了椭圆方程与几何性质等知识，为高考题的必考题，在近几年的各省高考题出现的频率较高

解题思路

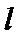
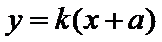
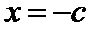
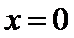
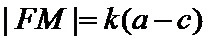
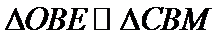
由题意设直线的方程为，分别令与得点，由，得

易错点

对椭圆方程与几何性质理解出现错误、计算错误

知识点

椭圆的定义及标准方程椭圆的几何性质直线、圆及圆锥曲线的交汇问题

热门试卷

正确答案

知识点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

知识点

正确答案

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点