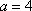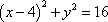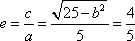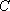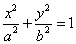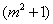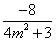- 椭圆的定义及标准方程
- 共448题
已知直线











(1)求椭圆
(2)(ⅰ) 设直线



(ⅱ)求线段
正确答案
见解析
解析
(1).椭圆 

(2)(ⅰ)设点

∴

∵点

∴
(ⅱ) 设直线

则

∵
∴ 直线

∴
故
∴
当且仅当

∴


知识点
在平面直角坐标,直线

(1)求椭圆E的方程;
(2)A、B、C是椭圆上的三个动点A与B关于原点对称,且|AC|=|CB|,问△ABC
的面积是否存在最小值?若存在,求此时点C的坐标;若不存在,说明理由。
正确答案
见解析。
解析
知识点
在平面直角坐标系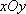

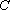
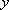
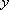
(1)求圆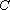
(2)若椭圆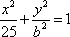


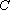
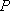
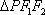
正确答案
见解析。
解析
解:(1)依题意,设圆的方程为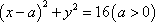
∵圆与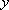
∴圆的方程为
(2)∵椭圆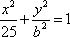
∴
解得
∴
∴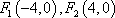
∴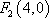
(i)过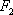

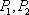

(ii)过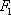
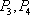
连接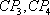
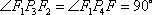
综上,圆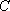
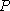
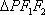
知识点
已知椭圆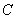
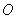
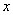
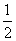
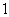
(1)求椭圆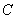
(2)若直线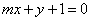

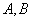
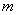
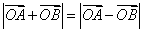
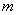
正确答案
见解析
解析
(1)设椭圆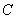
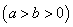

依题意
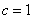
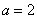
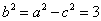
所以椭圆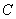

(2)不存在实数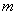
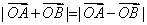
把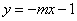
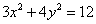
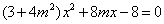
由于直线
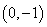
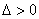
设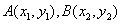
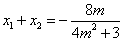
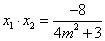
依题意,若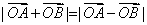
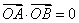
即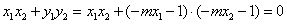
整理得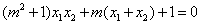
所以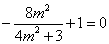
整理得
所以不存在实数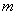

知识点
已知椭圆



(1)求椭圆
(2)若直线







正确答案
(1)
(2)
解析
(1)由已知椭圆的焦点在







(2)






设





设






将



知识点
扫码查看完整答案与解析