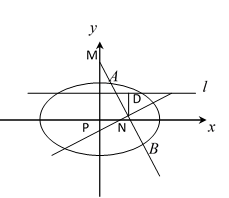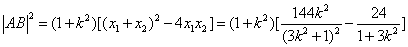- 椭圆的定义及标准方程
- 共448题
已知椭圆














(1) 求椭圆
(2) 是否存在满足



正确答案
见解析。
解析
(1) 解法1:设椭圆

依题意: 
∴ 椭圆

解法2:设椭圆

根据椭圆的定义得

∵

∴ 椭圆

(2)解法1:设点



∵
∴
∴
化简得:
由


∴抛物线



即
同理,抛物线



设点

而

代入②得 
则




若




∵直线


∴直线

∴满足条件

解法2:设点


由


∴抛物线



即
∵

∵点


同理, 
综合①、②得,点

∵经过
∴直线

∵点


∴点

若



∵直线


∴直线

∴满足条件

解法3:显然直线


由


设

由


∴抛物线



即
∵

同理,得抛物线



由
∴
∵
∴点

∴
化简得
由
可得方程(*)有两个不等的实数根. ∴满足条件的点
知识点
已知椭圆


(1)求椭圆
(2)过点















正确答案
见解析
解析
(1)依题得


所以椭圆

(2)根据已知可设直线

由

设

直线


令
则

所以

知识点
已知椭圆

(1)求椭圆C的方程;
(2)过椭圆C上的动点P引圆O:x2+y2=b2的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所
引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在, 请说明理由。
正确答案
见解析。
解析
(1)设椭圆的半焦距为c,依题意
∴b=2,
∴所求椭圆方程为
(2)如图,设P点坐标为(x0,y0),
若∠APB=900,则有
即
有
两边平方得
又因为P(x0,y0)在椭圆上,所以
①,②联立解得
所以满足条件的有以下四组解



所以,椭圆C上存在四个点



知识点
已知椭圆



(1)求椭圆
(2)过焦点












正确答案
见解析
解析
(1)依题设



由


所以椭圆

(2)依题直线

由

设



则



所以
直线

令


若四边形


所以
若点


整理得




此时点


知识点
已知椭圆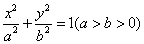
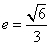
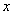
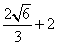
(1)求椭圆的标准方程;
(2)设点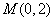
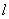
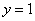
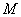
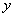
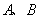
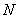
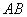
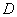
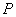
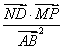
正确答案
见解析。
解析
(1)解:由题意可得
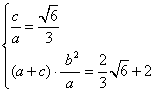
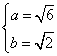
∴椭圆的标准方程为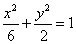
(2)设直线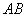
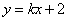
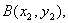
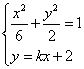
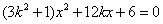
∵直线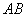
∴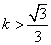
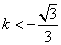
由
得
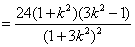
设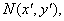
∴直线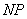
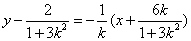
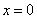
-----------------11分
∴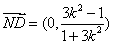
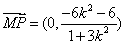
∴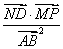
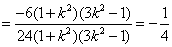
知识点
扫码查看完整答案与解析