- 导数的加法与减法法则
- 共661题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
若变量x,y满足约束条件
正确答案
-2
解析
画出可行域如图所示:
画直线l0:y=-2x,平移直线l0,当过A(k,k)时,使得z最小,由最小值为-6,可得3k=-6,解得k=-2.
知识点
设S为复数集C的非空子集.若对任意

①集合S={a+bi|(

②若S为封闭集,则一定有
③封闭集一定是无限集;
④若S为封闭集,则满足

其中真命题是 (写出所有真命题的序号)
正确答案
①②
解析
直接验证可知①正确。
当S为封闭集时,因为x-y∈S,取x=y,得0∈S,②正确
对于集合S={0},显然满足素有条件,但S是有限集,③错误
取S={0},T={0,1},满足
知识点
已知数列



(1) 若

(2) 设





(3)若




正确答案
见解析。
解析
(1)依题意,



综上可得
(2)由已知得

当



当



∴


∴
对于不等式



又当

∴
∴
当



即
∵
∴
综上,
(3)设公差为

∴

∴


∴

∴

解得

∴

知识点
已知数列{an}满足a1=1,|an+1-an|=pn,n∈N*.
(1)若{an}是递增数列,且a1,2a2,3a3成等差数列,求p的值;
(2)若
正确答案
见解析。
解析
(1)因为{an}是递增数列,所以an+1-an=|an+1-an|=pn.
而a1=1,因此a2=p+1,a3=p2+p+1.
又a1,2a2,3a3成等差数列,所以4a2=a1+3a3,
因而3p2-p=0,解得
当p=0时,an+1=an,这与{an}是递增数列矛盾。
故
(2)由于{a2n-1}是递增数列,因而a2n+1-a2n-1>0,于是(a2n+1-a2n)+(a2n-a2n-1)>0.①
但
由①,②知,a2n-a2n-1>0,
因此
因为{a2n}是递减数列,同理可得,a2n+1-a2n<0,故
由③,④即知,
于是an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)
=
=
=
故数列{an}的通项公式为
解题思路
对于第(1)问,根据{an}是递增数列,可将已知|an+1-an|=pn的绝对值符号去掉,再根据a1=1,用p表示出a2,a3来,然后由条件a1,2a2,3a3成等差数列,建立关于p的方程求出p的值,对于第(2)问,可先由已知条件{a2n-1}是递增数列与{a2n}是递减数列建立不等关系,再依据已知条件|an+1-an|=pn得出a2n-a2n-1与a2n+1-a2n的表达式,最后利用累加法,求出an.
知识点
某企业有甲、乙两个研发小组,他们研发新产品成功的概率分别为

(1)求至少有一种新产品研发成功的概率;
(2)若新产品A研发成功,预计企业可获利润120万元;若新产品B研发成功,预计企业可获利润100万元,求该企业可获利润的分布列和数学期望。
正确答案
见解析。
解析
记E={甲组研发新产品成功},F={乙组研发新产品成功},由题设知




且事件E与F,E与



(1)记H={至少有一种新产品研发成功},则

故所求的概率为
(2)设企业可获利润为X(万元),则X的可能取值为0,100,120,220.
因



故所求的分布列为
数学期望为

在第(1)问中,考虑到欲求概率的事件包含的互斥事件较多,因此可先求其对立事件的概率,再根据互为对立事件的概率之和为1,求得原事件的概率,在第(2)问中,先列出该企业所获利润的所有可能的取值,然后用相互独立事件的概率公式求出各个概率值,列出表格即得分布列,最后利用数学期望的定义求得期望值。
知识点
已知函数
(1) 当

(2)若

正确答案
见解析。
解析
(1)当b=4时,f(x)=(x2+4x+4)


则

由f′(x)=0,得x=﹣2或x=0。
当x<﹣2时,f′(x)<0,f(x)在(﹣∞,﹣2)上为减函数。
当﹣2<x<0时,f′(x)>0,f(x)在(﹣2,0)上为增函数。
当0<x<

∴当x=﹣2时,f(x)取极小值为0。
当x=0时,f(x)取极大值为4;
(2)由f(x)=(x2+bx+b)
=
由f(x)在区间(0,
得f′(x)≥0对任意x∈(0,
即﹣5x2﹣3bx+2x≥0对任意x∈(0,
∴

∵
∴
∴b的取值范围是
知识点
如图,用K、
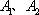
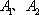
正确答案
解析
分两种情况:①K正常且
故
知识点
扫码查看完整答案与解析