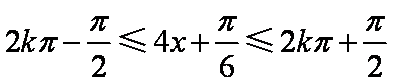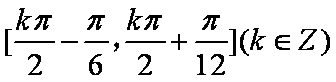- 导数的加法与减法法则
- 共661题
将甲、乙、丙、丁四名学生分到三个不同的班,每个班至少分到一名学生,且甲、乙两名学生不能分到一个班,则不同分法的种数为( )
正确答案
解析
∵每个班至少分到一名学生,且甲、乙两名学生不能分到一个班用间接法解四名学生中有两名学生分在一个班的种数是C42,元素还有一个排列,有A33种,而甲乙被分在同一个班的有A33种,
∴满足条件的种数是C42A33﹣A33=30,故选C。
知识点
将
正确答案
12
解析
先填第一行,则第一行有
知识点
已知极坐标系的极点与直角坐标系的原点重合,极轴与x轴的正半轴重合,若直线l的极坐标方程为
(1)把直线
(2)已知



正确答案
见解析。
解析
(1)直线


即


(2)








∴当


知识点
某班组织的数学文化节活动中,通过抽奖产生了







(1)求这


(2)设





正确答案
见解析。
解析
这




(1)要获得



则所求概率为
(2)




所以
故随机变量

知识点
已知函数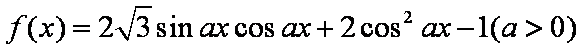
(1)求a的值;
(2)求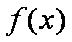
正确答案
见解析。
解析
(1)
令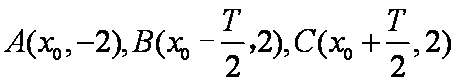
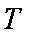
则
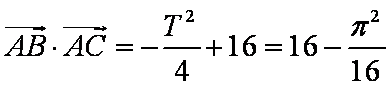
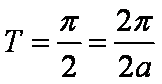
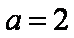
(2)因为
所以
解得
所以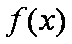
知识点
扫码查看完整答案与解析