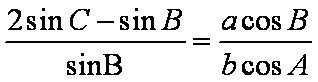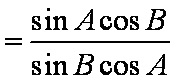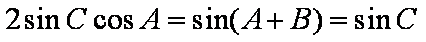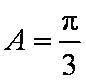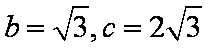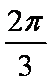- 导数的加法与减法法则
- 共661题
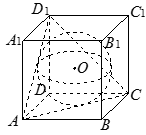
设


正确答案
解析
略
知识点
在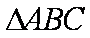
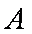
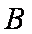

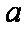
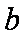
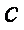
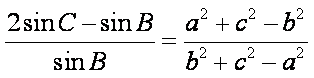
(1)求角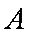
(2)若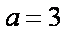
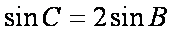
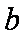
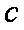
正确答案
见解析
解析
(1)由正弦定理得
所以
因为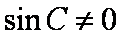
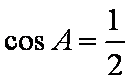
(2)由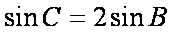
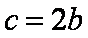
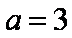
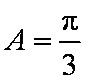
所以由余弦定理得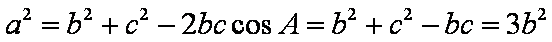
知识点
在





(1)求
(2)若

正确答案
见解析。
解析
(1)由题意,
得
由于





(2)由

即

得


∴

知识点
在复平面内,复数
正确答案
解析
略
知识点
如图所示,在四棱柱




(1)求证:
(2)若





正确答案
见解析
解析
方法一:(1)因为侧面

又
所以


(2)设线段














设



所以





由


设平面



得




又平面


故平面


方法二:(1)连接





连
由



所以



又根据菱形的性质


从而
(2)因为




延长





则






连接


由题意知


故


易知






故平面


知识点
设双曲线









正确答案
解析
略
知识点
已知函数
(1)当

(2)当函数

正确答案
见解析
解析
本题考查绝对值不等式解法、最值求解等基础知识,考查推理论证能力及运算求解能力。
(1)当

有不等式
当



当



当



综上函数

(2)∵函数


∴只要



即



知识点
已知抛物线的顶点是坐标原点







(1)求抛物线的方程;
(2)在



(3)若





正确答案
(1)y2=4x
(2)m<-1
(3)[-6,-2]∪[2,6]
解析
(1)设抛物线方程


联立消去


设


所以

所求抛物线方程为
(2)因为



由(1)得



所以



所以


解得

(3)由条件可设


所以




根据抛物线定义可知,以




知识点
如图,在三棱锥









(1)求证:

(2)求

(3)设点





正确答案
见解析
解析
(1)因为 



所以 
又因为 

所以 

又因为 

所以 
因为 

所以 
又因为 
所以 

(2)在平面

因为 



由 




所以以








设平面



由 



设



所以 
即 
(3)因为 


又因为 

因为 



所以 
解得 
知识点
如图,已知球
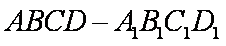
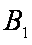
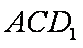

正确答案
解析


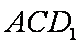
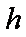

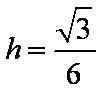
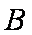
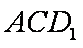
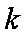
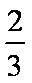
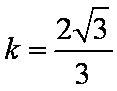
又球的半径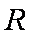
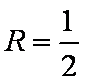
由勾股定理可知,截面圆的半径为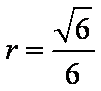
圆锥底面面积为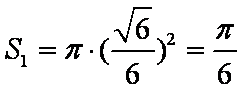
圆锥的母线可利用勾股定理求出: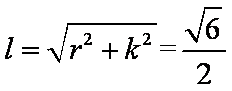
圆锥的侧面积为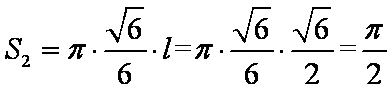
圆锥的表面积为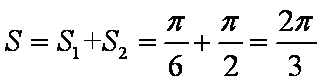
知识点
扫码查看完整答案与解析