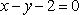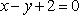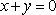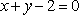- 导数的加法与减法法则
- 共661题
(1)若a=1,求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)求函数f(x)在[一2,2]上的最小值。
正确答案
见解析。
解析
(1)
知识点
已知直线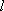
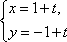
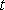
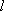
正确答案
解析
略
知识点
已知函数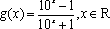
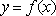
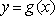
(1)求函数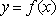
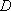
(2)设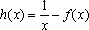
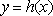
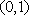
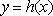
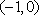

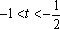
正确答案
见解析
解析
(1) 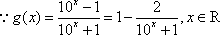
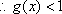
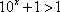
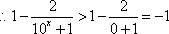
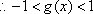
由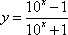
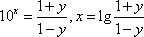
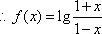
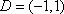
证明 (2)由(1)可知,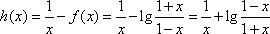
可求得函数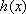

对任意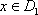
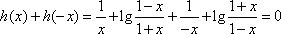
所以,函数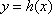
当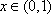

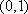
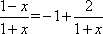
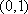
于是,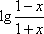
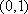
因此,函数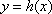
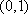
依据奇函数的性质,可知,
函数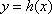
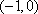
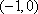
又
知识点
已知点P是△ABC的中位线EF上任意一点,且EF//BC,实数x,y满足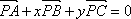
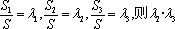
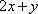
正确答案
解析
略。
知识点
已知函数



(1)求
(2)当


(3)证明:当



正确答案
见解析。
解析
(1)解:∵

∵直线


∴


(2)解法1:由(1)得
当



令

令

当




从而,当



故
因此,当


∴所求

解法2:由(1)得
当


令

方程

(ⅰ)当




故函数

由于
则当


(ⅱ)当



故函数


(ⅲ) 当


则



故函数


从而,函数


而
由(ⅱ)知,当

得

故当

综上所述,

(3)证明:由(2)得,当


又
从而,
把

知识点
已知等比数列







(1)求数列



(2)设

正确答案
见解析。
解析
(1) 解法一:由
由上式结合

则当


∵

∴数列

∴

【解法二:由
由上式结合

则当



∵


(2) 由

【或
∴
知识点
在




正确答案
解析
略。
知识点
已知函数


(1)当


(2)是否存在实数



正确答案
见解析
解析
(1)




则曲线在

(2)



当



当






令








知识点


正确答案
一或三
解析
略
知识点
已知点




正确答案
解析
设







知识点
扫码查看完整答案与解析