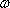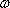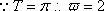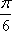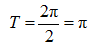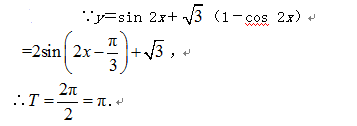抛物线焦点弦的性质
共82题

· 抛物线焦点弦的性质

抛物线焦点弦的性质
共82题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

如图，直三棱柱，，点M，N分别为和的中点。

（1）证明：∥平面;

（2）若二面角为直二面角，求的值。

正确答案

见解析

解析

（1）连结，由已知

三棱柱为直三棱柱，

所以为中点.又因为为中点

所以，又平面

平面，因此 ……6分

（2）以为坐标原点，分别以直线为轴，轴，轴建立直角坐标系，如图所示

设则，

于是，

所以，设是平面的法向量，

由得，可取

设是平面的法向量，

由得，可取

因为为直二面角，所以，解得……12分

知识点

抛物线焦点弦的性质

题型：填空题

填空题 · 5 分

如图，过圆外一点分别作圆的切线和割线交圆于,，且=7，是圆上一点使得=5，∠=∠, 则= .

正确答案

√35

解析

知识点

抛物线焦点弦的性质

题型：单选题

单选题 · 5 分

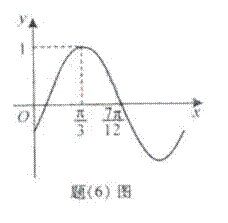
已知函数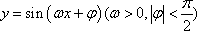的部分图象如题（6）图所示，则

A=1 =

B=1 =-

C=2 =

D=2 = -

正确答案

解析

由五点作图法知，= -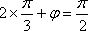

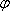
知识点

抛物线焦点弦的性质

题型：填空题

填空题 · 5 分

的展开式中的常数项为_________.

正确答案

-5

解析

的展开式的通项为，当r=3时，，当r=4时，，因此常数项为-20+15=-5

知识点

抛物线焦点弦的性质

题型：填空题

填空题 · 5 分

函数的最小正周期T为________

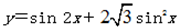
正确答案

解析

知识点

抛物线焦点弦的性质

题型：简答题

简答题 · 10 分

如图，⊙O和⊙相交于两点，过A作两圆的切线分别交两圆于C，D两点，连接DB并延长交⊙O于点E。

证明：

（1）；

（2）。

正确答案

见解析

解析

（1）由与相切于，得，同理，

所以。从而，即 ……4分

（2）由与相切于，得，又，得

从而，即，综合（1）的结论， ……10分

知识点

抛物线焦点弦的性质

题型：简答题

简答题 · 13 分

近年来，某市为促进生活垃圾的分类处理，将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类，并分别设置了相应的垃圾箱，为调查居民生活垃圾分类投放情况，先随机抽取了该市三类垃圾箱总计1000吨生活垃圾，数据统计如下（单位：吨）；

（1）试估计厨余垃圾投放正确的概率；

（2）试估计生活垃圾投放错误的概率；

（3）假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a，b，c，其中a﹥0，a+b+c=600.当数据a，b，c的方差s2最大时，写出a，b，c的值（结论不要求证明），并求此时s2的值。

（求：，其中为数据x1，x2，…，xn的平均数）

正确答案

（1）

（2）

（3）80000

解析

（1）由题意可知：。

（2）由题意可知：。

（3）由题意可知：，因此有当，，时，有。

知识点

抛物线焦点弦的性质

题型：单选题

单选题 · 5 分

对于数列，“”是“为递增数列”的【】

A必要不充分条件

B充分不必要条件

C充要条件

D既不充分也不必要条件

正确答案

解析

由知所有项均为正项，

且，即为递增数列

反之，为递增数列，不一定有，如-2，-1,0,1,2，…。

知识点

抛物线焦点弦的性质

题型：单选题

单选题 · 5 分

函数y＝ln(1－x)的定义域为(　　)。

A(0,1)

B[0,1)

C(0,1]

D[0,1]

正确答案

解析

要使函数有意义，需解得0≤x＜1，即所求定义域为[0,1)，故选B.

知识点

抛物线焦点弦的性质

题型：简答题

简答题 · 14 分

已知函数f（x）＝，a为常数且a>0.

（1）证明：函数f（x）的图像关于直线对称；

（2）若x0满足f（f（x0））＝x0，但f（x0）≠x0，则称x0为函数f（x）的二阶周期点，如果f（x）有两个二阶周期点x1，x2，试确定a的取值范围；

（3）对于（2）中的x1，x2和a，设x3为函数f（f（x））的最大值点，A（x1，f（f（x1））），B（x2，f（f（x2））），C（x3,0），记△ABC的面积为S（a），讨论S（a）的单调性。

正确答案

见解析

解析

（1）证明：因为＝a（1－2|x|），＝a（1－2|x|），

有，

所以函数f（x）的图像关于直线对称。

（2）解：当0＜a＜时，有f（f（x））＝

所以f（f（x））＝x只有一个解x＝0，又f（0）＝0，故0不是二阶周期点。

当时，有f（f（x））＝

所以f（f（x））＝x有解集，又当时，f（x）＝x，故中的所有点都不是二阶周期点。

当时，有f（f（x））＝所以f（f（x））＝x有四个解0，，又f（0）＝0，，，，故只有是f（x）的二阶周期点，综上所述，所求a的取值范围为.

（3）由（2）得，，

因为x3为函数f（f（x））的最大值点，所以，或.

当时，，求导得：

S′（a）＝，

所以当a∈时，S（a）单调递增，当a∈时S（a）单调递减；

当时，S（a）＝，求导得：

S′（a）＝，

因，从而有S′（a）＝>0，

所以当a∈时S（a）单调递增

知识点

抛物线焦点弦的性质

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 理科数学 > 抛物线焦点弦的性质

扫码查看完整答案与解析