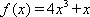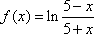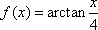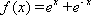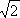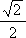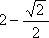- 抛物线焦点弦的性质
- 共82题
在区间


正确答案
1
解析
令



考察

故关于


知识点
函数

正确答案
解析
略
知识点
已知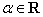
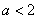
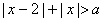
正确答案
解析
略。
知识点
函数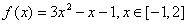
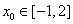
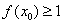
正确答案
解析
略。
知识点
能够把椭圆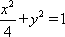
正确答案
解析
略
知识点
已知点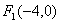
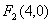
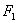
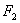
正确答案
解析
略
知识点
在直角坐标系xOy中,直线l过抛物线
正确答案
解析
由





知识点
在极坐标系中,直线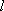
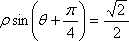
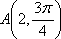
正确答案
解析
略
知识点
如图,











正确答案
2
解析
连接








又
∴
∴



知识点
己知⊙O:x2 +y2=6,P为⊙O上动点,过P作PM⊥x轴于M,N为PM上一点,且
(1)求点N的轨迹C的方程;
(2)若A(2,1),B(3,0),过B的直线与曲线C相交于D、E两点,则kAD+kAE是否为定值?若是,求出该值;若不是,说明理由。
正确答案
见解析
解析
(1)设



由


由于点







(2)设




由







知识点
扫码查看完整答案与解析