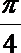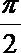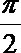- 抛物线焦点弦的性质
- 共82题
1
题型:
单选题
|
7.已知点









正确答案
D
解析
解析已在路上飞奔,马上就到!
知识点
抛物线的标准方程和几何性质抛物线焦点弦的性质直线与抛物线的位置关系
1
题型:填空题
|
13. 点













正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
抛物线的标准方程和几何性质抛物线焦点弦的性质
1
题型:填空题
|
5.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
抛物线焦点弦的性质
1
题型:
单选题
|
4. 函数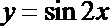

正确答案
B
解析
解析已在路上飞奔,马上就到!
知识点
抛物线焦点弦的性质
1
题型:简答题
|
23.已知函数f(x)=
(1)试就实数a的不同取值,写出该函数的单调递增区间;
(2)已知当a>0时,函数在(0,

(3)若函数f(x)在区间
正确答案
(1)①当a<0时,函数f(x)的单调递增区间为(﹣

②当0<a≤1时,函数f(x)的单调递增区间为(﹣∞,0)及(0,+∞),
③当a>1时,函数f(x)的单调递增区间为(﹣∞,﹣

(2)由题设及(1)中③知
且a>1,解得a=3,
因此函数解析式为f(x)=
(3)1#当a(a﹣1)>0即a<0或a>1时
由图象知
解得a∈(﹣∞,

2#当a=1时,函数为正比例函数,故在区间内存在反函数,所以a=1成立.
3#当a(a﹣1)<0,得到



综上a∈∈(﹣∞,



解析
解析已在路上飞奔,马上就到!
知识点
抛物线焦点弦的性质
已完结
扫码查看完整答案与解析